广东省东莞市2023-2024学年九年级上学期期末校际联盟数...

更新时间：2024-05-15 浏览次数：20 类型：期末考试

一、选择题（本大题共10小题，每小题3分，共30分。在每小题给出的四个选项中，只有一项是符合题目要求的）

1. (2024九上·东莞期末) 下列图案既是轴对称图形又是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2024九上·东莞期末) 事件A＝扔一枚硬币，结果正面朝上是（　　）

A . 必然事件 B . 确定事件 C . 随机事件 D . 不可能事件

答案解析收藏纠错 + 选题
3. (2024九上·东莞期末) 用配方法解方程x²﹣2x﹣5＝0时，原方程变形正确的是（　　）

A . （x﹣1）²＝6 B . （x﹣2）²＝9 C . （x+1）²＝6 D . （x+2）²＝9

答案解析收藏纠错 + 选题
4. (2024九上·东莞期末) 在平面直角坐标系中，将二次函数y＝（x﹣1）²+1的图象向下平移2个单位长度，所得函数的解析式为（　　）

A . y＝（x﹣2）²﹣1 B . y＝（x﹣1）²﹣1 C . y＝x²+1 D . y＝x²﹣1

答案解析收藏纠错 + 选题
5. (2024九上·东莞期末) 已知⊙O的半径为10，若PO＝6，则点P与⊙O的位置关系是（　　）

A . 点P在⊙O内 B . 点P在⊙O上 C . 点P在⊙O外 D . 无法判断

答案解析收藏纠错 + 选题
6. (2024九上·东莞期末) 在一个不透明的布袋中装有50个黄、白两种颜色的球，除颜色外其他都相同，小红通过多次摸球试验后发现，摸到黄球的频率稳定在0.3左右，则布袋中白球可能有( )

A . 15个 B . 20个 C . 30个 D . 35个

答案解析收藏纠错 + 选题
7. (2024九上·东莞期末) 九年级某学生对自己某次实心球训练的录像进行分析，发现实心球飞行高度y（米）与水平距离x（米）之间的关系为y＝ $\text{[math]}$ ，由此可知该生此次实心球训练的成绩为（　　）

A . 6米 B . 10米 C . 12米 D . 15米

答案解析收藏纠错 + 选题
8. (2024九上·东莞期末) 已知关于x的一元二次方程（k﹣2）x²﹣2x+1＝0有两个不相同的实数根，则k的值可能是（　　）

A . 0 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
9. (2024九上·东莞期末) 如图，过x轴正半轴任意一点P作x轴的垂线，分别与反比例函数 $\text{[math]}$ 和 $\text{[math]}$ 的图象交于点A和点B ．若点C是y轴上任意一点，连接AC、BC ，则△ABC的面积为（　　）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
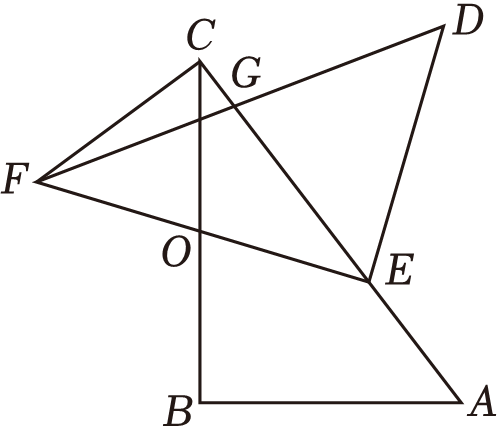
10. (2024九上·东莞期末) 如图，在Rt△ABC中，∠B＝90°，AB＝6，BC＝8，把△ABC绕BC边的中点O旋转后得△DEF ，若直角顶点E恰好落在AC边上，且DF边交AC边于点G ，则CG的长为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题（本大题共5小题，每小题3分，共15分）

11. (2024九上·东莞期末) 在函数 $\text{[math]}$ 中，自变量x的取值范围是．

答案解析收藏纠错 + 选题
12. (2024·沙田模拟) 在平面直角坐标系中，点（2，﹣3）关于原点的对称点坐标为．

答案解析收藏纠错 + 选题
13. (2024九上·东莞期末) 若m是方程x²﹣3x+1＝0的一个根，则代数式2m²﹣6m+1＝．

答案解析收藏纠错 + 选题
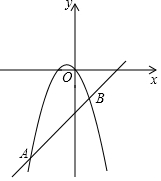
14. (2024九上·东莞期末) 如图，抛物线y＝ax²+bx与直线y＝mx+n相交于点A（﹣3，﹣6），B（1，﹣2），则关于x的不等式ax²+bx＞mx+n的解集为．

答案解析收藏纠错 + 选题
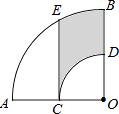
15. (2024九上·东莞期末) 如图，在扇形AOB中，∠AOB=90°，点C为OA的中点，CE⊥OA交 $\text{[math]}$ 于点E，以点O为圆心，OC的长为半径作 $\text{[math]}$ 交OB于点D．若OA=2，则阴影部分的面积为．

答案解析收藏纠错 + 选题

三、解答题一（本大题共2小题，每小题5分，共10分）

16. (2024九上·东莞期末) 解方程：3x²+4x＝2．

答案解析收藏纠错 + 选题
17. (2024九上·东莞期末) 如图，方格纸中的每个小正方形的边长都为1，在建立平面直角坐标系后，△ABC的顶点均在格点上．
1. （1）以点A为旋转中心，将△ABC绕点A顺时针旋转90°得到△AB₁C₁ ，画出△AB₁C₁ ．
2. （2）画出△ABC关于原点O成中心对称的△A₂B₂C₂ ．
答案解析收藏纠错 + 选题

四、解答题二（本大题共3小题，每小题7分，共21分）

18. (2024九上·东莞期末) 现今网购已经成为消费的新常态，某快递公司今年8月份的投递快递总件数为10万件，由于改进分拣技术，增加投递业务人员，10月份的投递快递总件数达到12.1万件，假设该公司每个月的投递快递总件数平均增长率相同．
1. （1）求该公司的投递快递总件数月平均增长率；
2. （2）如果继续保持上面的月平均增长率，平均每个业务员每月最多可投递快递0.7万件，那么20名投递业务员能否完成今年11月份的快递投递任务？说明理由．
答案解析收藏纠错 + 选题
19. (2024九上·东莞期末) 小明与小红在玩转盘游戏时，把转盘A、B分别分成4等份、3等份，并在每一份内标上数字，如图所示．游戏规定：转动转盘停止后，指针必须指到某一数字，否则重转．
1. （1）小明转动转盘B ，转到的数字是偶数的概率为：；
2. （2）现游戏规则为：转盘A转出的数字记为x ，转盘B转出的数字记为y ，若x ， y满足xy＞6，则小明胜，若xy＜6，则小红胜，请用列表法或画树状图的方法说明这个游戏规则对双方是否公平．
答案解析收藏纠错 + 选题
20. (2024九上·东莞期末) 如图，⊙O的直径AB垂直弦CD于点E ， F是圆上一点，D是 $\text{[math]}$ 的中点，连结CF交OB于点G ，连结BC ．
1. （1）求证：GE＝BE；
2. （2）若AG＝6，BG＝4，求CD的长．
答案解析收藏纠错 + 选题

五、解答题三（本大题共3小题，每小题8分，共24分）

21. (2024九上·东莞期末) 如图，一次函数y＝kx+b的图象与反比例函数 $\text{[math]}$ 的图象交于点A（m ， 4），与x轴交于点B ，与y轴交于点C（0，3）．
1. （1）求m的值和一次函数的表达式；
2. （2）已知P为反比例函数 $\text{[math]}$ 图象上的一点，S_△_OBP＝12，求点P的坐标．
答案解析收藏纠错 + 选题
22. (2024九上·东莞期末) 如图，正方形ABCD的边长为5，点E为正方形CD边上一动点，过点B作BP⊥AE于点P ，将AP绕点A逆时针旋转90°得AP^' ，连接P^'D ．
1. （1）求证：PB＝P^'D；
2. （2）若DF＝1，求线段AP的长度．
答案解析收藏纠错 + 选题
23. (2024九上·东莞期末) 某商场购进一种每件成本为80元的新商品，在商场试销发现：销售单价x（元/件）与每天销售量y（件）之间满足如图所示的关系：
1. （1）求出y与x之间的函数关系式；
2. （2）疫情期间，有关部门规定每件商品的利润率不得超过25%，那么将售价定为多少，来保证每天获得的总利润最大，最大总利润是多少？
3. （3）在试销过程中，受国家扶持，每销售一件新产品，国家补贴商场a元（0＜a≤5），并要求包含补贴后每件的利润不高于36元，通过销售记录发现：每件补贴经费a元后，每天销售的总利润仍随着售价的增大而增大，求出a的取值范围．
答案解析收藏纠错 + 选题

六、解答题四（本大题共2小题，每小题10分，共20分）

24. (2024九上·东莞期末) 如图，在△PBD中，PO平分∠BPD ， DE⊥PO交PO延长线于点E ， ∠EDB＝∠EPB ，以OB为半径的⊙O的交BD于点A ，已知PB＝6，DB＝8．
1. （1）求证：PB是⊙O的切线．
2. （2）求⊙O的半径．
3. （3）连接BE ，求BE的长．
答案解析收藏纠错 + 选题
25. (2024九上·东莞期末) 如图，在平面直角坐标系中，已知抛物线y＝ax²+bx+2与x轴相交于A（﹣1，0），B（4，0）两点，与y轴交于点C ．
1. （1）求抛物线的解析式；
2. （2）点P是直线BC上方抛物线上一动点，连接PB ， PC ，求△PBC面积的最大值以及此时点P的坐标；
3. （3）抛物线上是否存在点Q ，使∠QCB＝45°？若存在，请直接写出点Q的坐标；若不存在，请说明理由．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

广东省东莞市2023-2024学年九年级上学期期末校际联盟数...

副标题：

*注意事项：

广东省东莞市2023-2024学年九年级上学期期末校际联盟数...

试题分析

总体分析

题量分析

难度分析

知识点分析