浙江省温州市龙湾九校联考2023-2024学年九年级下学期数...

更新时间：2024-05-22 浏览次数：25 类型：开学考试

一、选择题：本大题有10个小题，每小题3分，共30分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1. (2024九下·龙湾开学考) 已知⊙O的半径为7，点A在⊙O外，则OA的长可能是（）

A . 5 B . 6 C . 7 D . 8

答案解析收藏纠错 + 选题
2. (2024九下·龙湾开学考) 任意抛掷一枚均匀的骰子，骰子停止转动后，下列事件中，发生可能性最小的是（）

A . 朝上一面的点数是3 B . 朝上一面的点数是3的倍数 C . 朝上一面的点数小于3 D . 朝上一面的点数大于3

答案解析收藏纠错 + 选题
3. (2024九下·龙湾开学考) 如图，点D，E分别在△ABC的AB，AC边上，且DE∥BC，若CE∶AE＝2∶3，BC＝10，则DE的长为（）

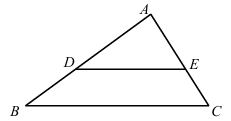
A . 4 B . 5 C . 6 D . 7

答案解析收藏纠错 + 选题
4. (2024九下·龙湾开学考) 如图，已知四边形ABCD内接于⊙O，∠ADC＝144°，则∠AOC的大小是（）

A . 36° B . 72° C . 46° D . 92°

答案解析收藏纠错 + 选题
5. (2024九下·龙湾开学考) 关于二次函数y＝－x²＋2x－3的图象，下列说法正确的是（）

A . 对称轴是直线x＝－1 B . 当x＞﹣1时，y随x的增大而减小 C . 顶点坐标为（－1，－2） D . 图象与x轴没有交点

答案解析收藏纠错 + 选题
6. (2024九下·龙湾开学考) 如图是一个游戏转盘，自由转动转盘，当转盘停止转动后，指针不落在“I”所示区域的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024九下·龙湾开学考) 摄影中有一种拍摄手法叫黄金构图法，原理如下：如图，在正方形ABCD的BC边上取中点 $\text{[math]}$ ，以点 $\text{[math]}$ 为圆心，线段DE长为半径作圆，交BC的延长线于点 $\text{[math]}$ ，过点 $\text{[math]}$ 作FG $\text{[math]}$ ，交AD的延长线于点 $\text{[math]}$ ，得到矩形CDGF.若 $\text{[math]}$ ，则CF的长为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024九下·龙湾开学考) 如图，已知点 $\text{[math]}$ 在以AC为直径的 $\text{[math]}$ 上，过 $\text{[math]}$ 作 $\text{[math]}$ 交 $\text{[math]}$ 于 $\text{[math]}$ ，连结BC，CD，AD，AD与BC交于点 $\text{[math]}$ .若 $\text{[math]}$ ，则AC的长是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 3 D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2024九下·杭州月考) 关于 $\text{[math]}$ 的二次函数 $\text{[math]}$ .甲同学认为：若 $\text{[math]}$ ，则当 $\text{[math]}$ 时， $\text{[math]}$ 随 $\text{[math]}$ 的增大而增大.乙同学认为：若该二次函数的图象在 $\text{[math]}$ 轴上截得的线段长为3，则 $\text{[math]}$ 的值是1或 $\text{[math]}$ .以下对两位同学的看法判断正确的是（）

A . 甲、乙都错误 B . 甲、乙都正确 C . 甲正确、乙错误 D . 甲错误、乙正确

答案解析收藏纠错 + 选题
10. (2024九下·龙湾开学考) 方方同学将图①中圆形纸片沿直径AB向上对折得到图②，再沿弦BC向下翻折得到图③，最后沿弦BD翻折得到图④.若点E恰为弧BD的中点，则AD：DB的值为（）

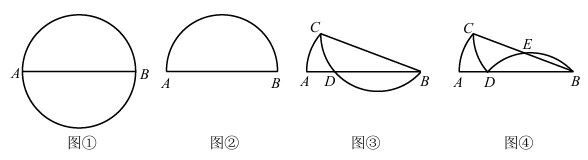
A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题:本大题有6个小题,每小题3分,共18分.

11. (2024九下·龙湾开学考) 若 $\text{[math]}$ ，则 $\text{[math]}$ 的值为.

答案解析收藏纠错 + 选题
12. (2024九下·龙湾开学考) 已知圆心角为 $\text{[math]}$ 的扇形的孤长为 $\text{[math]}$ ，则该扇形的面积为.

答案解析收藏纠错 + 选题
13. (2024九下·龙湾开学考) 将抛物线 $\text{[math]}$ 先向右平移3个单位，再向上平移2个单位，得到新抛物线的顶点坐标为.

答案解析收藏纠错 + 选题
14. (2024九下·龙湾开学考) 如图， $\text{[math]}$ 的半径是5，点 $\text{[math]}$ 是弦AB延长线上的一点，连结OC，若 $\text{[math]}$ $\text{[math]}$ ，则BC的长为.

答案解析收藏纠错 + 选题
15. (2024九上·绍兴月考) 如图，已知抛物线 $\text{[math]}$ （a、b均不为0)与双曲线 $\text{[math]}$ 的图象相交于 $\text{[math]}$ 三点.则不等式 $\text{[math]}$ 的解是.

答案解析收藏纠错 + 选题
16. (2024九下·龙湾开学考) 我国伟大的数学家刘徽在《九章算术注》中指出，“周三径一”不是圆周率值，实际上是圆内接正六边形周长和直径的比值．刘徽发现，圆内接正多边形边数无限增加时，多边形的周长就无限逼近圆周长，从而创立“割圆术”，为计算圆周率建立起相当严密的理论和完善的算法．如图，六边形ABCDEF是圆内接正六边形，把每段弧二等分，可以作出一个圆内接正十二边形，点G为弧CD的中点，连结BG，GF，FC，BG交CF于点P，则△PGF与△PBC的面积之比为.

答案解析收藏纠错 + 选题

三、解答题：本大题有8个小题，共72分.解答应写出文字说明、证明过程或演算步骤.

17. (2024九上·余杭月考) 一个不透明的袋子中装有3个完全相同的小球（只有颜色不同），其中1个红球，2个白球．从中任意摸出一个小球，记下颜色后放回，搅匀后再摸出一个小球，记下颜色．圆圆同学认为“两次摸出的小球颜色只有两种结果，要么相同，要么不同，所以两次摸出的小球颜色相同的概率是 $\text{[math]}$ ”．你认为圆圆的看法正确吗？请用画树状图或列表法说明理由．

答案解析收藏纠错 + 选题
18. (2024九下·龙湾开学考) 如图，在由边长为1的小正方形构成的6×8的网格中，△ABC的顶点A，B，C均在格点上．请按要求完成作图：①仅用无刻度直尺；②保留作图痕迹并标注相关字母．
1. （1）如图1，在线段AC上找一点D，使得 $\text{[math]}$ .
2. （2）如图2，画出△ABC的角平分线BE．
答案解析收藏纠错 + 选题
19. (2024九下·龙湾开学考) 如图，在矩形ABCD中，点E在边CD上，连结AE，过点B作BF⊥AE于点F．
1. （1）求证：△ABF∽△EAD．
2. （2）若AB＝10，BC＝6，DE＝3，求BF的长度．
答案解析收藏纠错 + 选题
20. (2024九下·龙湾开学考) 设二次函数y＝ax²＋bx＋c（a，b，c是实数，且a≠0）．已知函数值y和自变量x的部分对应取值如表所示：
x
…
-1
0
1
2
3
…
y
…
-8
-3
0
1
0
…
1. （1）求二次函数的表达式．
2. （2）若点M（m，n）是抛物线上一点，且0≤m≤4，求n的取值范围．
答案解析收藏纠错 + 选题
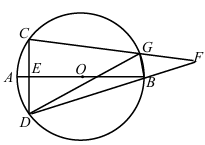
21. (2024九下·龙湾开学考) 如图，AB是⊙O的直径，弦CD⊥AB于点E，点F在DB延长线上，连结CF交⊙O于点G，连结DG，BG．
1. （1）若弧AC度数是36°，求∠BGD的度数．
2. （2）求证：∠BGD＝∠BGF．
答案解析收藏纠错 + 选题
22. (2024九下·龙湾开学考) 如图，四边形ABCD是平行四边形，点E是BA延长线上一点，连结DE，BD，CE，CE分别与AD，BD交于点F，G．
1. （1）若BE＝3CD，BC＝12，求AF的长．
2. （2）求证：GC²＝GF·GE．
答案解析收藏纠错 + 选题
23. (2024九下·龙湾开学考) 如图，已知四边形ABCD内接于⊙O，对角线AC，BD交于点E，AC＝BD，AC⊥BD．
1. （1）猜想∠ACB的度数，并说明理由．
2. （2）若⊙O的半径为10，∠BCD=60°，求四边形ABCD的面积．
3. （3）若过圆心O作OF⊥BC于点F．求证：AD＝2OF．
答案解析收藏纠错 + 选题
24. (2024九下·龙湾开学考) 在二次函数复习课上，李老师为检验同学们对函数知识的掌握情况，给出一个关于 $\text{[math]}$ 的函数 $\text{[math]}$ .下面是方方同学的探究过程，请予以补充完整.
1. （1）当 $\text{[math]}$ 时，对于函数 $\text{[math]}$ 随 $\text{[math]}$ 的增大而，且 $\text{[math]}$ .对于函数 $\text{[math]}$ 随 $\text{[math]}$ 的增大而，且 $\text{[math]}$ .结合上述分析，可以发现对于函数 $\text{[math]}$ ，当 $\text{[math]}$ 时， $\text{[math]}$ 随 $\text{[math]}$ 的增大而.
2. （2）当 $\text{[math]}$ 时，对于函数 $\text{[math]}$ ，取若干自变量 $\text{[math]}$ 与函数 $\text{[math]}$ 的对应值如下表：
  $\text{[math]}$
  0
  $\text{[math]}$
  1
  $\text{[math]}$
  2
  $\text{[math]}$
  3
  $\text{[math]}$
  $\text{[math]}$
  0
  $\text{[math]}$
  $\text{[math]}$
  $\text{[math]}$
  $\text{[math]}$
  $\text{[math]}$
  5
  $\text{[math]}$
  求 $\text{[math]}$ 的值，并在给出的平面直角坐标系中画出当 $\text{[math]}$ 时函数 $\text{[math]}$ 的图象.
3. （3）过点 $\text{[math]}$ 作平行于 $\text{[math]}$ 轴的直线 $\text{[math]}$ ，请结合(1)(2)的分析，当直线 $\text{[math]}$ 与函数 $\text{[math]}$ 的图象有两个交点时，求 $\text{[math]}$ 的取值范围.
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

浙江省温州市龙湾九校联考2023-2024学年九年级下学期数...

副标题：

*注意事项：

浙江省温州市龙湾九校联考2023-2024学年九年级下学期数...

试题分析

总体分析

题量分析

难度分析

知识点分析

$\text{[math]}$	0	$\text{[math]}$	1	$\text{[math]}$	2	$\text{[math]}$	3	$\text{[math]}$
$\text{[math]}$	0	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	5	$\text{[math]}$

x	…	-1	0	1	2	3	…
y	…	-8	-3	0	1	0	…