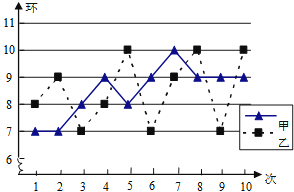
在某次训练中,甲、乙两名射击运动员各射击10发子弹的成绩统计图如图所示,对于本次训练,有如下结论:①S甲2>S乙2;②S甲2<S乙2;③甲的射击成绩比乙稳定;④乙的射击成绩比甲稳定,由统计图可知正确的结论是( )

|
平均成绩/环 |
中位数/环 |
众数/环 |
方差 |
|
|
甲 |
a |
7 |
7 |
1.2 |
|
乙 |
7 |
b |
8 |
c |
从中位数的角度来比较,成绩较好的是;从众数的角度来比较,成绩较好的是;成绩相对较稳定的是.
ⅰ.甲、乙两种型号扫地机器人除尘指数的折线图:
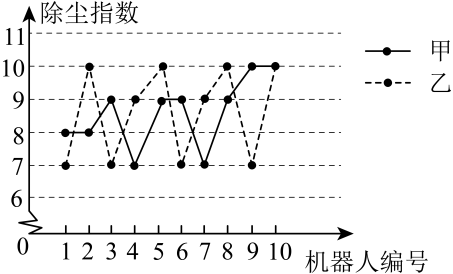
ⅱ.丙型号扫地机器人的除尘指数数据:10,10,10,9,9,8,3,9,8,10.
ⅲ.甲、乙、丙三种型号机器人除尘指数的平均数:
| 扫地机器人 | 甲 | 乙 | 丙 |
| 除尘指数平均数 | 8.6 | 8.6 | m |
根据以上信息,回答下列问题:
测试项目 | 创新能力 | 专业知识 | 语言表达 |
测试成绩(分) | 70 | 80 | 92 |

这三项成绩按照如图所示的比例确定综合成绩,则该应聘者最后的得分为分.

两位同学四项成绩分布的条形统计图
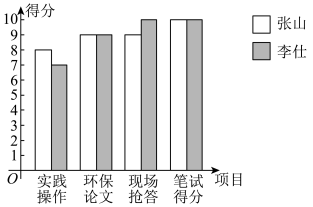
姓名 | 平均数(分) | 中位数(分) | 众数(分) | 方差(分2) |
张山 | 9 | 9 | ||
李仕 | 9.5 | 1.5 |
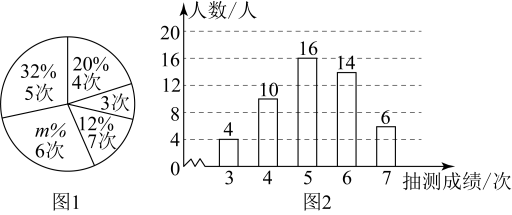
书活动的情况,随机调查了部分学生每人参加活动的项目数量,根据统计的结果,绘制出如下统计图,
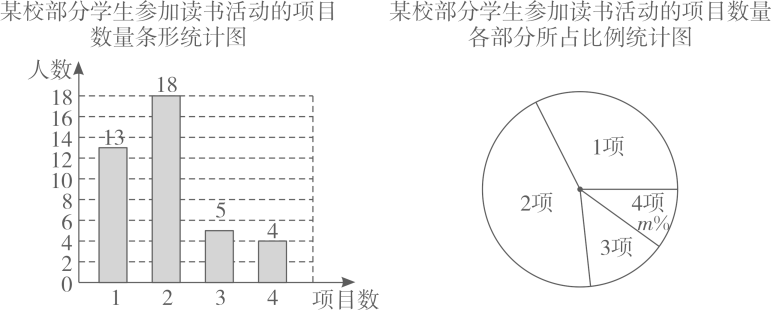
请根据相关信息,解答下列问题:
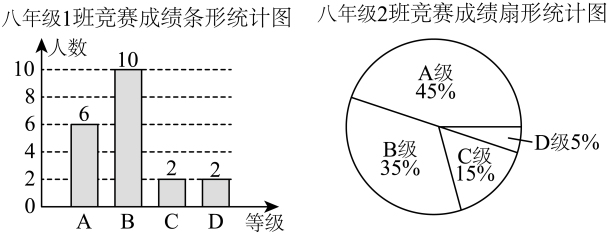
班级 | 平均数 | 众数 | 中位数 |
八年级1班 | 分 | 90分 | 分 |
八年级2班 | 92分 | 分 | 90分 |
【收集数据】小明最近8次的米和立定跳远成绩.
次数 项目 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| | | | | | | | |
立定跳远(米) | | | | | | | | |
【整理数据】依据中考标准分数表将1000米和立定跳远的成绩转化成相应分数,并绘制成折线统计图如图所示.
米和立定跳远的中考标准分数表(部分)
项目 分值 | | 立定跳远(米) |
9分 | | |
8分 | | |
7分 | | |
6分 | | |
5分 | | |
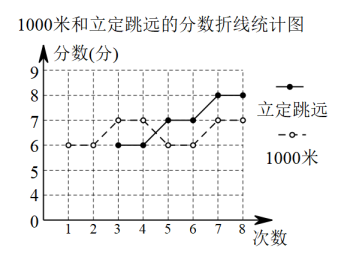
【应用数据】

初赛阶段两个年级各10名选手的成绩统计如下:
七年级:98 96 86 85 84 94 77 69 59 94
八年级:99 96 73 82 96 79 65 96 55 96
他们的数据分析过程如下:

请补全八年级频数分布直方图;
年级 | 平均数 | 中位数 | 方差 |
七年级 | ① | 85.5 | 144.36 |
八年级 | 83.7 | ② | 251.21 |
根据以上数据求出表格中①,②两处的数据;