一、单项选择题:本题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有一项是符合题目要求的。每小题选出答案后,用铅笔把答题卡上对应题目的答案涂黑。如需改动,用橡皮擦干净后,再选涂其他答案。
-
1.
(2024·横县月考)
在

中,角
A ,
B ,
C所对的边分别为
a ,
b ,
c , 若

, 则角
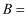
( )
-
-
A . 3
B .  C . 2
D .
C . 2
D . 
-
-
5.
(2024·横县月考)
如图,正四棱锥

底面的四个顶点
A ,
B ,
C ,
D在球
O的同一个大圆上,点
P在球面上.若

, 则球
O的体积是( )
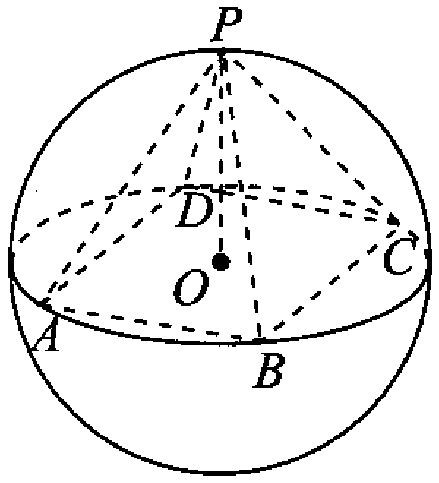
-
-
-
A .  平面ACGD
B .
平面ACGD
B .  平面ABED
C .
平面ABED
C .  D . 平面
D . 平面 平面CGF
平面CGF
二、多项选择题:本题共4小题,每小题5分,共20分。在每小题给出的四个选项中,有多项是符合题目要求,全部选对得5分,部分选对得3分,错选不得分。每小题选出答案后,用铅笔把答题卡上对应题目的答案涂黑。如需改动,用橡皮擦干净后,再选涂其他答案。
三、填空题:本题共4小题,每小题5分,共20分。
-
13.
(2024·横县月考)
设

,

是不共线的向量,若

,

,

,
A ,
B ,
D三点共线,则

的值为
.
-
-
15.
(2024·横县月考)
已知α,β是两个不同的平面,m、n是平面α及β之外的两条不同直线,给出四个论断:①m⊥n;②α⊥β;③n⊥β;④m⊥α.以其中三个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:
.
-
16.
(2024·横县月考)
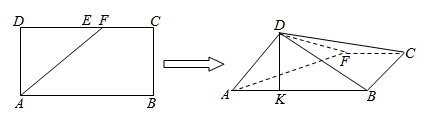
如图,在长方形ABCD中,AB=2,BC=1,E为DC的中点,F为线段EC(端点除外)上一动点,现将△AFD沿AF折起,使平面ABD⊥平面ABC,在平面ABD内过点D作DK⊥AB,K为垂足,设AK=t,则t的取值范围是
.
四、解答题:本题共6小题,共70分。解答应写出文字说明,证明过程或演算步骤。
-
-
(1)
证明:

.
-
(2)
若D为BC的中点,从①

, ②

, ③

这三个条件中选取两个作为条件证明另外一个成立.
注:若选择不同的组合分别解答,则按第一个解答计分.
-
-
(1)
求

;
-
(2)
当

时,求实数
m.
-
-
-
(2)
若圆锥内有一球与圆锥的底面及圆锥的所有母线都相切,求此球的表面积.
-
20.
(2024·横县月考)
如图①,已知等边三角形
ABC的边长为3,点
M ,
N分别是边
AB ,
AC上的点,且

,

.如图②,将

沿
MN折起到

的位置.
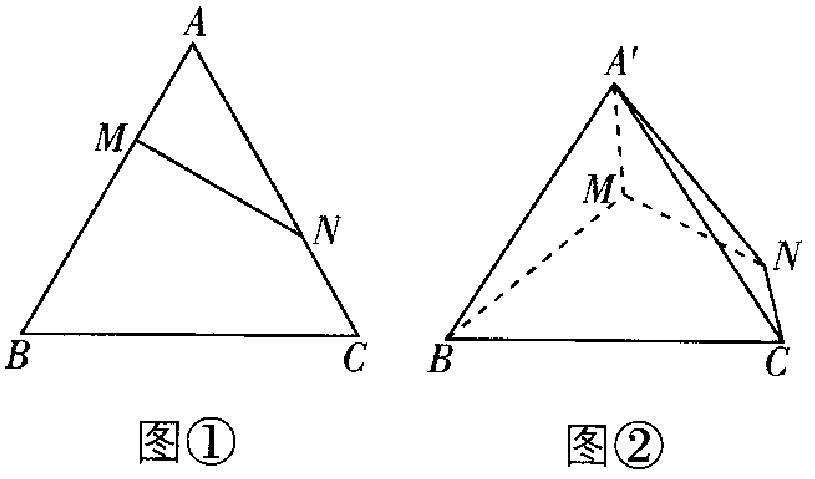
-
(1)
求证:平面

平面
BCNM.
-
-
-
(1)

平面
ABC;
-
(2)
当
E为

的垂心时,求证:

是直角三角形.
-
22.
(2024·横县月考)
在我国古代数学名著《九章算术》中将由四个直角三角形组成的四面体称为“鳖臑”.已知三棱锥

中,

平面
ABC.

-
(1)
从三棱锥

中选择合适的两条棱填空.若

,则该三棱锥为“鳖臑”.
-
(2)
已知三棱锥

是一个“鳖臑”,且

,

,

.
①若 上有一点D , 如图①所示,试在平面PAC内作出一条过点D的直线l , 使得l与BD垂直,说明作法,并给予证明;
上有一点D , 如图①所示,试在平面PAC内作出一条过点D的直线l , 使得l与BD垂直,说明作法,并给予证明;
②若点D在线段PC上,点E在线段PB上,如图②所示,且 平面EDA , 证明
平面EDA , 证明 是平面EAD与平面BAC的二面角的平面角.
是平面EAD与平面BAC的二面角的平面角.

;②二面角
的大小为的大小为
;③
到平面BCNM的距离为
.
上是否存在一点P , 使三棱锥
的体积为
?若存在,求出
的值,若不存在,请说明理由.
上有一点D , 如图①所示,试在平面PAC内作出一条过点D的直线l , 使得l与BD垂直,说明作法,并给予证明;
平面EDA , 证明
是平面EAD与平面BAC的二面角的平面角.