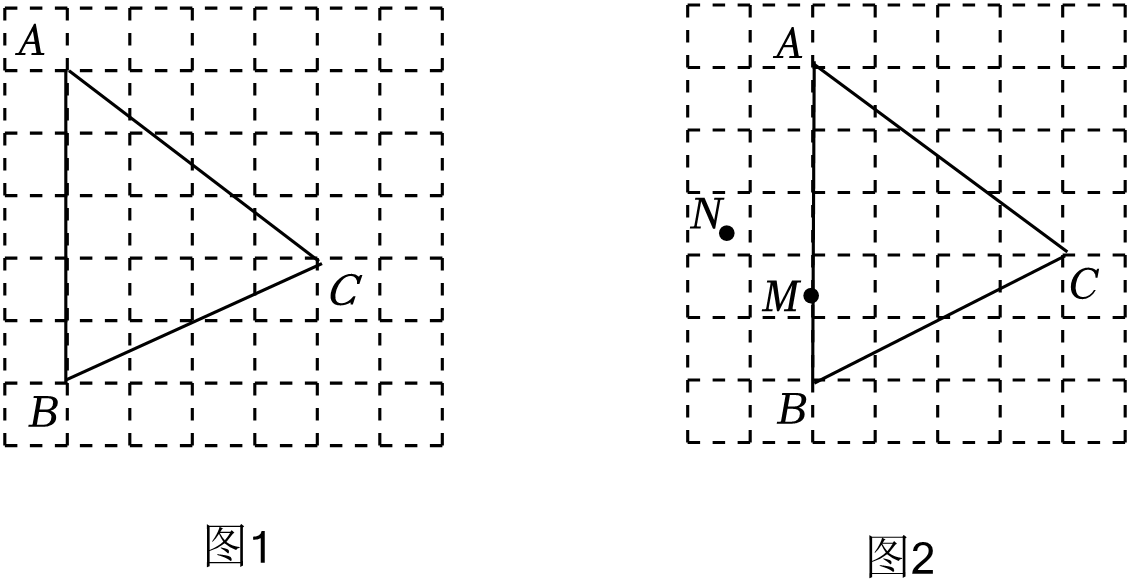
B .
B .  C .
C .  D .
D . 

 B .
B .  C .
C .  D .
D . 鸭的质量/千克 | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 |
烤制时间/分钟 | 40 | 60 | 80 | 100 | 120 | 140 | 160 | 180 |
设鸭的质量为x千克,烤制时间为t . 估计当x=3.8千克时,t的值约为( )


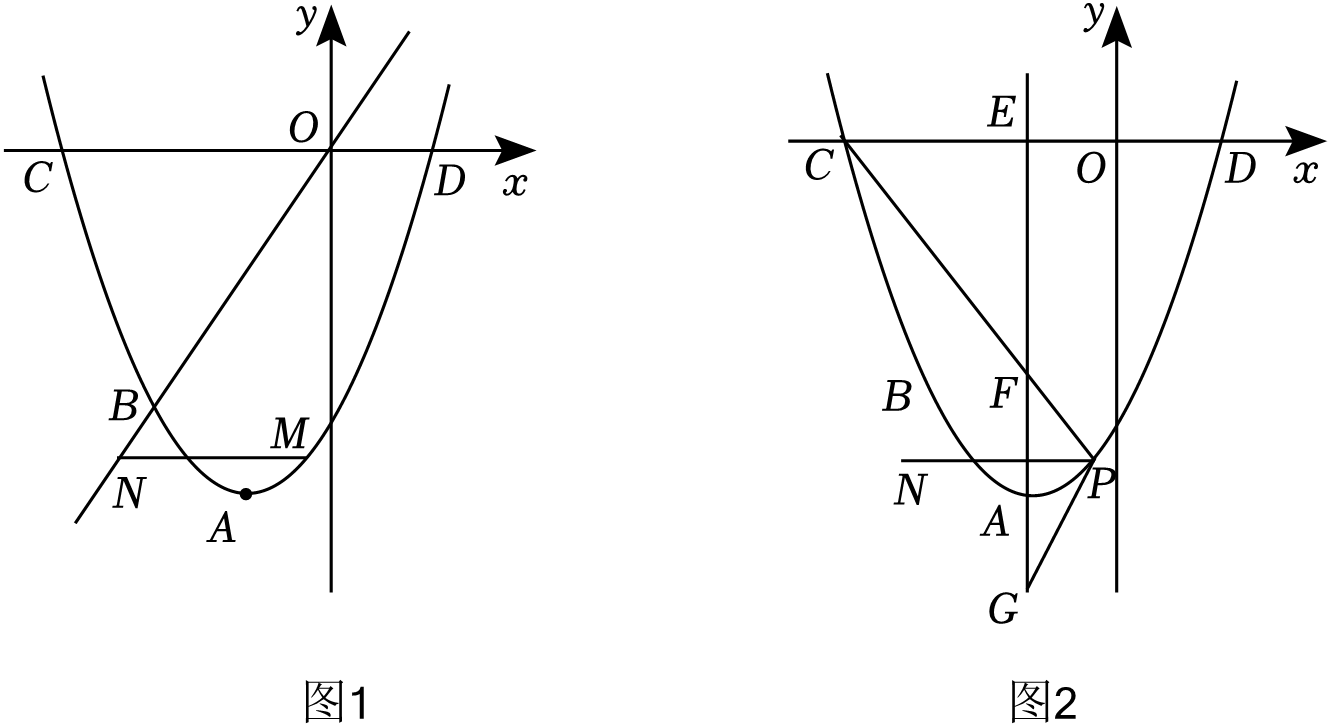
①一元二次方程ax2+bx+c=0的根为x1=﹣2,x2=6;
②若点C(﹣5,y1)、D(π,y2)在该抛物线上,则y1>y2;
③对于任意实数t , 总有at2+bt≥4a+2b;
④对于a的每一个确定值(a>0),若一元二次方程ax2+bx+c=p(p为常数)有根,则p≥1﹣16a , 其中正确的结论是 .(填写序号)
身高情况分组表
组别 | A | B | C | D | E |
身高(cm) | x<155 | 155≤x<160 | 160≤x<165 | 165≤x<170 | x≥170 |
根据图表提供的信息,回答下列问题: