浙江省北斗星盟2023-2024学年高三下学期适应性联考数学...

更新时间：2024-07-04 浏览次数：28 类型：高考模拟

一、单项选择题：本题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的.

1. (2024·浙江模拟) 已知集合 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024·浙江模拟) 已知复数 $\text{[math]}$ 满足 $\text{[math]}$ ，则复数 $\text{[math]}$ 在复平面内对应的点位于（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
3. (2024·浙江模拟) 已知向量 $\text{[math]}$ ， $\text{[math]}$ ，若 $\text{[math]}$ 与 $\text{[math]}$ 垂直，则 $\text{[math]}$ 等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 3 D . 6

答案解析收藏纠错 + 选题
4. (2024·浙江模拟) 已知数列 $\text{[math]}$ 满足 $\text{[math]}$ ，则“ $\text{[math]}$ 为等比数列”是“ $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ ）”的（）

A . 充分条件但不是必要条件 B . 必要条件但不是充分条件 C . 充要条件 D . 既不是充分条件也不是必要条件

答案解析收藏纠错 + 选题
5. (2024·浙江模拟) 在对某校高三学生体质健康状况某个项目的调查中，采用样本量比例分配的分层随机抽样，如果不知道样本数据，只知道抽取了男生80人，女生120人，其方差分别为15，10，由此估计样本的方差不可能为（）

A . 11 B . 13 C . 15 D . 17

答案解析收藏纠错 + 选题
6. (2024·浙江模拟) 若 $\text{[math]}$ ，则（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024·浙江模拟) 如图，假定两点 $\text{[math]}$ ， $\text{[math]}$ 以相同的初速度运动.点 $\text{[math]}$ 沿直线 $\text{[math]}$ 作匀速运动， $\text{[math]}$ ；点 $\text{[math]}$ 沿线段 $\text{[math]}$ （长度为 $\text{[math]}$ 单位）运动，它在任何一点的速度值等于它尚未经过的距离（ $\text{[math]}$ ）.令 $\text{[math]}$ 与 $\text{[math]}$ 同时分别从 $\text{[math]}$ ， $\text{[math]}$ 出发，定义 $\text{[math]}$ 为 $\text{[math]}$ 的纳皮尔对数，用现在的数学符号来叙述， $\text{[math]}$ 与 $\text{[math]}$ 的对应关系就是 $\text{[math]}$ （ $\text{[math]}$ ），当点 $\text{[math]}$ 从线段 $\text{[math]}$ 靠近 $\text{[math]}$ 的三等分点移动到靠近 $\text{[math]}$ 的三等分点，经过的时间为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
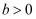
8. (2024·浙江模拟) 设双曲线 $\text{[math]}$ ： $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ ）的左焦点为 $\text{[math]}$ ，过坐标原点的直线与 $\text{[math]}$ 交于 $\text{[math]}$ ， $\text{[math]}$ 两点， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的离心率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、多项选择题：本题共3小题，每小题6分，共18分.在每小题给出的选项中，有多项符合题目要求，全部选对的得6分，部分选对的得部分分，有选错的得0分.

9. (2024·浙江模拟) 已知函数 $\text{[math]}$ ，则（）

A . $\text{[math]}$ 的最小正周期为 $\text{[math]}$ B . $\text{[math]}$ 的图像关于 $\text{[math]}$ 对称 C . $\text{[math]}$ 在 $\text{[math]}$ 上单调递减 D . 当 $\text{[math]}$ 时， $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2024·浙江模拟) 已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 是一个随机试验中的三个事件，且 $\text{[math]}$ ， $\text{[math]}$ ，下列说法正确的是（）

A . 若 $\text{[math]}$ 与 $\text{[math]}$ 互斥，则 $\text{[math]}$ 与 $\text{[math]}$ 不相互独立 B . 若 $\text{[math]}$ 与 $\text{[math]}$ 相互独立，则 $\text{[math]}$ 与 $\text{[math]}$ 不互斥 C . 若 $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ 与 $\text{[math]}$ 相互独立 D . 若 $\text{[math]}$ ，则 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 两两独立

答案解析收藏纠错 + 选题
11. (2024·浙江模拟) 已知正方体 $\text{[math]}$ 的棱长为1，点 $\text{[math]}$ 满足 $\text{[math]}$ ，其中 $\text{[math]}$ ， $\text{[math]}$ ，则（）

A . 当 $\text{[math]}$ 时，则 $\text{[math]}$ 的最小值为 $\text{[math]}$ B . 过点 $\text{[math]}$ 在平面 $\text{[math]}$ 内一定可以作无数条直线与 $\text{[math]}$ 垂直 C . 若 $\text{[math]}$ 与 $\text{[math]}$ 所成的角为 $\text{[math]}$ ，则点 $\text{[math]}$ 的轨迹为双曲线 D . 当 $\text{[math]}$ ， $\text{[math]}$ 时，正方体经过点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 的截面面积的取值范围为 $\text{[math]}$

答案解析收藏纠错 + 选题

三、填空题：本题共3小题，每小题5分，共15分.

12. (2024·浙江模拟) 若 $\text{[math]}$ 展开式的二项式系数之和为128，则展开式中 $\text{[math]}$ 的系数为.

答案解析收藏纠错 + 选题
13. (2024·浙江模拟) 已知圆 $\text{[math]}$ ： $\text{[math]}$ 和圆 $\text{[math]}$ ： $\text{[math]}$ ，过圆 $\text{[math]}$ 上一动点 $\text{[math]}$ 作圆 $\text{[math]}$ 的切线，交圆 $\text{[math]}$ 于 $\text{[math]}$ ， $\text{[math]}$ 两点，当 $\text{[math]}$ （点 $\text{[math]}$ 为坐标原点）面积最大时，满足条件的切线方程为.（写出一条即可）

答案解析收藏纠错 + 选题
14. (2024·浙江模拟) 已知函数 $\text{[math]}$ ， $\text{[math]}$ ，对任意 $\text{[math]}$ ，存在 $\text{[math]}$ 使得不等式 $\text{[math]}$ 成立，则满足条件的 $\text{[math]}$ 的最大整数为.

答案解析收藏纠错 + 选题

四、解答题：本题共5小题，共77分。解答应写出文字说明、证明过程或演算步骤.

15. (2024·浙江模拟) 在直角坐标平面内有线段 $\text{[math]}$ ，已知点 $\text{[math]}$ 是线段 $\text{[math]}$ 上靠近 $\text{[math]}$ 的三等分点，点 $\text{[math]}$ 是线段 $\text{[math]}$ 上靠近 $\text{[math]}$ 的三等分点，……，点 $\text{[math]}$ 是线段 $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ ）上靠近 $\text{[math]}$ 的三等分点，设点 $\text{[math]}$ 的横坐标为 $\text{[math]}$ .
1. （1）求证：数列 $\text{[math]}$ 为等比数列；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的通项公式.
答案解析收藏纠错 + 选题
16. (2024·浙江模拟) 在四棱锥 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 、 $\text{[math]}$ 分别为直线 $\text{[math]}$ ， $\text{[math]}$ 上的动点.
1. （1）若异面直线 $\text{[math]}$ 与 $\text{[math]}$ 所成的角为45°，判断 $\text{[math]}$ 与 $\text{[math]}$ 是否具有垂直关系并说明理由；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求直线 $\text{[math]}$ 与平面 $\text{[math]}$ 所成角的最大值.
答案解析收藏纠错 + 选题
17. (2024·浙江模拟) 将除颜色外完全相同的红球2个、白球3个放入一盲盒（一种具有随机属性的玩具盒子），现从中不放回取球.
1. （1）若每次取一个球，求：
  （ⅰ）前两次均取到红球的概率；
  （ⅱ）第2次取到红球的概率；
2. （2）若从中取出两个球，已知其中一个球为红球，求：
  （ⅰ）另一个也为红球的概率；
  （ⅱ）若你现在可以选择从剩下的球中随机取一个球来替换另一个球，如果从提高取到红球的可能性出发，你是选择换还是不换？试说明理由.
答案解析收藏纠错 + 选题
18. (2024高二下·临川月考) 在平面直角坐标系 $\text{[math]}$ 中，已知点 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为动点，满足 $\text{[math]}$ .
1. （1）求动点 $\text{[math]}$ 的轨迹 $\text{[math]}$ 的方程；
2. （2）已知过点 $\text{[math]}$ 的直线 $\text{[math]}$ 与曲线 $\text{[math]}$ 交于两点 $\text{[math]}$ ， $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ .
  （ⅰ）记直线 $\text{[math]}$ ， $\text{[math]}$ 的斜率分别为 $\text{[math]}$ ， $\text{[math]}$ ，求证： $\text{[math]}$ 为定值；
  （ⅱ）直线 $\text{[math]}$ ， $\text{[math]}$ 与直线 $\text{[math]}$ 分别交于 $\text{[math]}$ ， $\text{[math]}$ 两点，求 $\text{[math]}$ 的最小值.
答案解析收藏纠错 + 选题
19. (2024·浙江模拟) 莫比乌斯函数，由德国数学家和天文学家莫比乌斯提出，数学家梅滕斯首先使用 $\text{[math]}$ 作为莫比乌斯函数的记号，其在数论中有着广泛应用.所有大于1的正整数 $\text{[math]}$ 都可以被唯一表示为有限个质数的乘积形式： $\text{[math]}$ （ $\text{[math]}$ 为 $\text{[math]}$ 的质因数个数， $\text{[math]}$ 为质数， $\text{[math]}$ ， $\text{[math]}$ ），例如： $\text{[math]}$ ，对应 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .现对任意 $\text{[math]}$ ，定义莫比乌斯函数 $\text{[math]}$ .
1. （1）求 $\text{[math]}$ ， $\text{[math]}$ ；
2. （2）已知 $\text{[math]}$ ，记 $\text{[math]}$ （ $\text{[math]}$ 为 $\text{[math]}$ 的质因数个数， $\text{[math]}$ 为质数， $\text{[math]}$ ， $\text{[math]}$ ）的所有因数从小到大依次为 $\text{[math]}$ ， $\text{[math]}$ ， …， $\text{[math]}$ .
  （ⅰ）证明： $\text{[math]}$ ；
  （ⅱ）求 $\text{[math]}$ 的值（用 $\text{[math]}$ （ $\text{[math]}$ ）表示）.
答案解析收藏纠错 + 选题