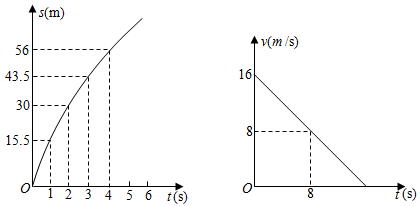
| x | … | -1 | 0 | 2 | 4 | 5 | … |
| y1 | … | 0 | 1 | 3 | 5 | 6 | … |
| y2 | … | 0 | -1 | 0 | 5 | 9 | … |
当y2>y1时,自变量x的取值范围是( )

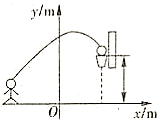
下列四个结论:①;②
;③当
时,若点
在该抛物线上,则
;④若关于x的一元二次方程
有两个相等的实数根,则
.
其中正确的是(填序号即可).

智能浇灌系统使用方案 | ||||
材料 |
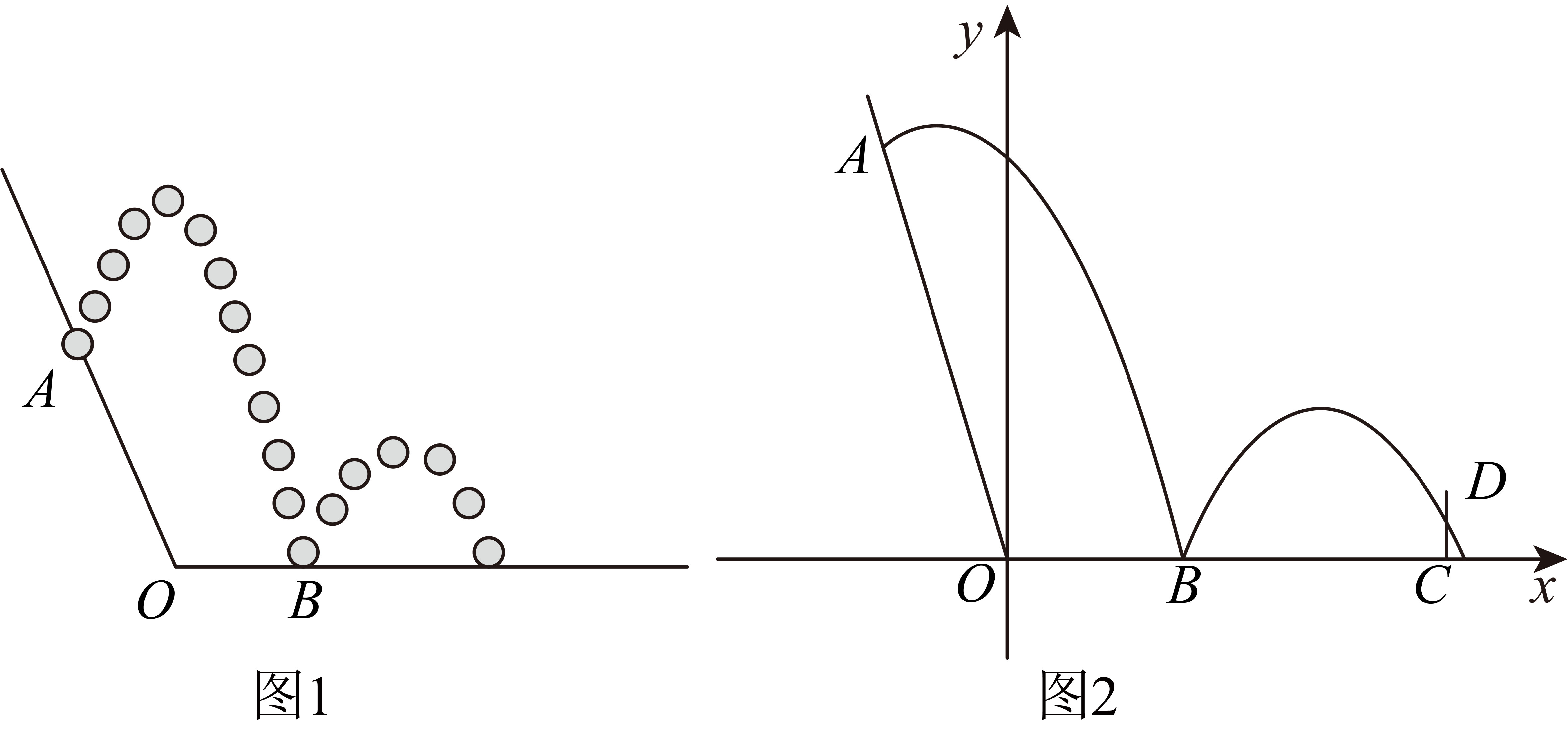
| 如图1是一款智能浇灌系统,水管OP垂直于地面并可以随意调节高度(OP最大高度不超过2.4m),浇灌花木时,喷头P处会向四周喷射水流形成固定形状的抛物线,水流落地点M与点O的距离即为最大浇灌距离,各方向水流落地点形成一个以点O为圆心,OM为半径的圆形浇灌区域. 当喷头P位于地面与点O重合时,某一方向的水流上边缘形成了如图2的抛物线,经测量, 如图3,农科院将该智能浇灌系统应用于一个长8m,宽6m的矩形试验田中,水管放置在矩形中心O处. | ||
问题解决 | ||||
任务1 | 确定水流形状 | 在图2中建立合适的平面直角坐标系,求抛物线的函数表达式. | ||
任务2 | 探究浇灌最大区域 | 当调节水管OP的高度时,浇灌的圆形区域面积会发生变化,请你求出最大浇灌圆形区域面积.(结果保留 | ||
任务3 | 解决具体问题 | 若要保证浇灌区域能完全覆盖矩形试验田,则水管OP至少需要调节到什么高度? | ||
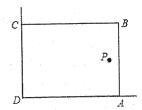
【知识背景】如图,校园中有两面直角围墙,墙角内的P处有一古棵树与墙 ,
的距离分别是
和
, 在美化校园的活动中,某数学兴趣小组想借助围墙(两边足够长),用
长的篱笆围成一个矩形花园
(篱笆只围
,
两边),设
.
【方案设计】设计一个矩形花园,使之面积最大,且要将古棵树P围在花园内(含边界,不考虑树的粗细).
【解决问题】思路:把矩形的面积S与边长x(即
的长)的函数解析式求出,并利用函数的性质来求面积的最大值即可.