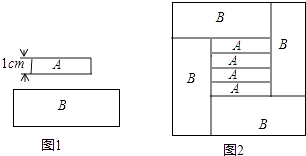

按照曹冲称象的方法:先将象牵到大船上,并在船的侧面标记水位再将象牵出,然后往船上抬入20块等重的条形石,并在船上留3个搬运工,这时水位恰好到达标记位置,如果再抬入1块同样的条形石,船上只留1个搬运工,水位也恰好到达标记的位置,已知搬运工体重为130kg , 求大象的体重?设每块条形石的质量为x kg , 依题意列方程得( )

原价 | 优惠 |
不超过100元 | 不打折 |
超过100元但不超过300元 | 八折 |
超过300元 | 六折 |
参赛者 | 答对题数 | 答错题数 | 得分 |
A | 20 | 0 | 100 |
B | 19 | 1 | 94 |
C | 18 | 2 | 88 |
D | 14 | 6 | 64 |
E | 10 | 10 | 40 |

则张叔叔家到银行的距离是 。

步骤:计算前
位数字中偶数位数字的和
, 即
;
步骤:计算前
位数字中奇数位数字的和
, 即
;
步骤:计算
与
的和
, 即
;
步骤:取大于或等于
且为
的整数倍的最小数
, 即
;
步骤:计算
与
的差就是校验码
, 即
.
如图,若条形码中被污染的两个数字的和是 , 则被污染的两个数字中右边的数字是.
| 月使用费/元 | 主叫限定时间/min | 主叫超时费/(元/min) | 被叫 |
A套餐 | 38 | 100 | 0.2 | 免费 |
B套餐 | 98 | 500 | 0.25 | 免费 |
其中,月使用费固定收,主叫不超过限定时间不再收费,主叫超过部分加收超时费,被叫免费.
方案一:买一副羽毛球拍送一桶羽毛球;
方案二:羽毛球拍和羽毛球都按定价的90%付款.
现某羽毛球培训学校要到该超市购买羽毛球拍5副,羽毛球x桶(x>5):
若该校按方案二购买,需付款元.(用含x的代数式表示);
A方法:剪6个侧面;B方法:剪4个侧面和5个底面。
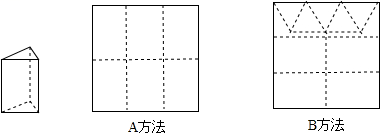
现有19张硬纸板,裁剪时x张用A方法,其余用B方法。
侧面:个,底面:个
学习了一元一次方程之后,数学兴趣小组了解到如下信息:
我国的铁路旅客列车,按不同的进行速度、运行范围、设备配置、作业特征等,分为不同的级别,列车的级别由车次开头的字母来表示(部分是纯数字).如G字头,表示高速动车组旅客列车;D字动,表示动车组旅客列车;C字头,表示城际旅客列车;K学头,表示快速旅客列年,等等.随着交通的发展吕梁站至太原南站已并通了多次列车,其中“C150”次列车的平均速度是120km/h,“K1334”次列车的平均速度是90km/h,并且“C150”次列车从吕梁站至太原南站所时间比“K1334”次列车少用30分钟(两列车中途停留时间均除外).
兴趣小组提出了以下两个问题:
小彬列的方程是“”
任务一:①小彬同学所列方程中的x表示 ▲ ,
②小彬同学列方程所用的数量关系为 ▲ (“路程÷速度=时间“除外);
任务二:小亮的做法是:设“K1334”次列车从吕梁站至太原南站所用时间为y小时,请你帮助小亮解决上述两个问题,写出解答过程.