【培优卷】湘教版（2024）七年级上册3.7二元一次方程组的...

更新时间：2024-09-09 浏览次数：10 类型：同步测试

一、选择题

1. (2024七下·赣州期末) 如图，约定：上方相邻的左数与右数之差等于这两数下方箭头共同指向的数．有以下两个结论，结论I：若m的值为3，则y的值为4；结论Ⅱ：不论m ， n取何值， $\text{[math]}$ 的值一定为3．下列说法正确的是（）

A . I，Ⅱ都对 B . I对，Ⅱ不对 C . I不对，Ⅱ对 D . I，Ⅱ都不对

答案解析收藏纠错 + 选题
2. 小明分别以两种形式储蓄了共 5000 元，第一种储蓄的年利率为 $\text{[math]}$ ，第二种储蓄的年利率为 $\text{[math]}$ ，一年后得到的利息和为 156 元．那么小明以这两种形式储蓄的钱数分别是（）

A . 2000 元和 3000 元
B . 3000 元和 2000 元
C . 1000 元和 4000 元
D . 4000 元和 1000 元

答案解析收藏纠错 + 选题
3. (2024七下·永定期中) 我国古典数学文献《增删算法统宗•六均输》中有一个“隔沟计算”的问题：“甲乙隔沟牧放，二人暗里参详．甲云得乙九只羊，多乙一倍之上，乙说得甲九只，两家之数相当，二人闲坐恼心肠，画地算了半晌”其大意为：甲，乙两人一起放牧，两人心里暗中数羊．如果乙给甲9只羊，那么甲的羊数为乙的2倍；如果甲给乙9只羊，那么两人的羊数相同．请问甲，乙各有多少只羊？设甲有羊x只，乙有羊y只，根据题意列方程组正确的为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024七下·义乌月考) 如图3，在大长方形中放置9个形状、大小相同的小长方形，则图中阴影部分面积和为（）（说明：图中的单位为 $\text{[math]}$ ）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2024七下·威远期中) 果树基地安排26名工人将采摘的水果包装成果篮，每个工人每小时可包装200个苹果或者300个梨，每个果篮中放3个苹果和2个梨．为了使包装的水果刚好完整配成果篮，应该安排多少名工人包装苹果，多少名工人包装梨？设安排x名工人包装苹果，y名工人包装梨，可列方程组为（　　）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2024七下·朝阳月考) 在“幻方拓展课程”探索中，小明在如图的3×3方格内填入了一些表示数的代数式，若图中各行、各列及对角线上的三个数之和都相等，则x﹣y=(　　　)

A . 2 B . 4 C . 6 D . 8

答案解析收藏纠错 + 选题
7. (2022七下·合阳期末) 在《九章算术》中，一次方程组是由算筹布置而成的．如图1所示的算筹图，表示的方程组就是 $\text{[math]}$ 类似地，图2所示的算筹图表示的方程组为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2022七下·慈溪期中) 用如图 $\text{[math]}$ 中的长方形和正方形纸板作侧面和底面，做成如图 $\text{[math]}$ 的竖式和横式的两种无盖纸盒.现有 $\text{[math]}$ 张正方形纸板和 $\text{[math]}$ 张长方形纸板，如果做两种纸盒若干个，恰好将纸板用完，则 $\text{[math]}$ 的值可能是（）

A . 2019 B . 2020 C . 2021 D . 2022

答案解析收藏纠错 + 选题

二、填空题

9. 如图 1，有若干片相同的拼图，若将其沿相同方向无缝隙地拼在一起，他们的底部位于同一条直线上．当分别用 3 片、 10 片拼图时（如图 2，3 所示），对应的长度分别为 $\text{[math]}$ ， $\text{[math]}$ ，则图 1 中的拼图长为 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
10. (2024七下·杭州期中) 用如图1中的长方形和正方形纸板作侧面和底面，做成如图2的竖式和横式两种无盖纸盒．现在仓库里有1000张正方形纸板和■张长方形纸板．若做了竖式纸盒x个，横式纸盒y个，恰好将库存的纸板用完．小聪在做作业时，发现题中长方形纸板数字被墨水污染了，只记得这个数字比2000略大些，是2001，2002，2003，2004，2005中某个数字，则这个数字是，按照上述条件，按照上述条件，最后做成的横式纸盒比竖式纸盒多个

答案解析收藏纠错 + 选题
11. (2022七下·东阳期末) 在学完书中例题后，小聪想用现有的硬纸板裁成如图①的长方形和正方形作为侧面与底面，做成如图②的竖式和横式两种无盖纸盒.已知一张硬纸板的裁剪方式有两种（均有余料）），方式一：裁成3个长方形与一个正方形：方式二：裁成2个长方形与2个正方形.现小聪将m张硬纸板用方式一裁剪，n张硬纸板用方式二裁剪，则：
1. （1）两种方式共裁出长方形张，正方形张（用m、n的代数式表示）；
2. （2）当10＜m＜15时，所裁得的长方形与正方形纸板恰好用完，做成的两种无盖纸盒一共可能是个.
答案解析收藏纠错 + 选题
12. (2018七上·鄞州期中) 如图，两个形状、大小完全相同的大长方形内放入四个如图③的小长方形后分别得到如图①、图②、已知大长方形的长为a，则图②阴影部分周长与图①阴影部分周长的差是．

答案解析收藏纠错 + 选题
13. 如下图所示，高速公路上，一辆长为4米，速度为110千米/时的轿车准备超越一辆长为12米，速度为100千米/时的卡车，则轿车从开始追赶到超越卡车，需要花费的时间约是秒（结果保留整数）.

答案解析收藏纠错 + 选题

三、解答题

14. (2024七下·新晃期中) 某工厂准备在春节前生产甲、乙两种型号的新年礼盒共60万套，两种礼盒的成本和售价如下表所示．

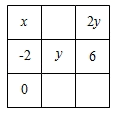
甲
乙
成本（元/套）
20
24
售价（元/套）
25
30
1. （1）该工厂计划筹集资金1340万元，且全部用于生产甲、乙两种礼盒，则这两种礼盒各生产多少万套？
2. （2）经过市场调查，该厂决定在原计划的基础上增加生产甲种礼盒m万套，增加生产乙种礼盒n万套（m ， n都为正整数），且两种礼盒售完后所获得的总利润恰为400万元，请问该工厂有几种生产方案？并写出所有可行的生产方案．
答案解析收藏纠错 + 选题
15. (2019七下·南县期末) 某企业在“蜀南竹海”收购毛竹，直接销售，每吨可获利100元，进行粗加工，每天可加工8吨，每吨可获利800元；如果对毛竹进行精加工，每天可加工1吨，每吨可获利4000元．由于受条件限制，每天只能采用一种方式加工，要求将在一月内（30天）将这批毛竹93吨全部销售．为此企业厂长召集职工开会，让职工讨论如何加工销售更合算．
甲说：将毛竹全部进行粗加工后销售；

乙说：30天都进行精加工，未加工的毛竹直接销售；

丙说：30天中可用几天粗加工，再用几天精加工后销售；

请问厂长应采用哪位说的方案做，获利最大？

答案解析收藏纠错 + 选题
16. (2023·长沙模拟) 阅读下列材料：
《张丘建算经》是一部数学问题集，其内容、范围与《九章算术》相仿．其中提出并解决了一个在数学史上非常著名的不定方程问题，通常称为“百鸡问题”：“今有鸡翁一值钱五，鸡母一值钱三，鸡雏三值钱一．凡百钱买鸡百只，问鸡翁、母、雏各几何．”

译文：每一只公鸡值五文钱，每一只母鸡值三文钱，每三只小鸡值一文钱．现在用一百文钱买一百只鸡，问这一百只鸡中，公鸡、母鸡、小鸡各有多少只？

结合你学过的知识，解决下列问题：
1. （1）若设母鸡有x只，公鸡有y只，
  ① 小鸡有只，买小鸡一共花费文钱；（用含x ， y的式子表示）
  
  ②根据题意，列出一个含有x ， y的方程：；
2. （2）若对“百鸡问题”增加一个条件：母鸡数量是公鸡数量的4倍多2只，求此时公鸡、母鸡、小鸡各有多少只?
3. （3）除了问题（2）中的解之外，请你再直接写出两组符合“百鸡问题”的解．
答案解析收藏纠错 + 选题
17. (2024七上·遵义期末) 某校七年级组在学习《一元一次方程》时开展了以“节约用电”为主题的项目化学习，本项目的驱动问题：居民用电是如何计费的，选择峰谷电合算吗？
过程探究1：了解某省电网销售电价：
单位：元/千瓦时（含税）

普通电价
峰时电价
谷时电价
第一阶梯：年用电量2760千瓦时及以下部分
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
第二阶梯：年用电量2761-4800千瓦时部分
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
第三阶梯：年用电量4801千瓦时及以上部分
$\text{[math]}$
$\text{[math]}$
$\text{[math]}$
备注：居民生活用电分时电价时段划分：高峰时段： $\text{[math]}$ ，低谷时段： $\text{[math]}$ 次日 $\text{[math]}$ ．
过程探究2：月用电量300千瓦时需缴多少钱的电费？（分类大讨论）
第一大组
第二大组
不使用峰谷电：
① $\text{[math]}$ 元
② $\text{[math]}$ 元
③ $\text{[math]}$ 元
使用峰谷电（若其中峰电150千瓦时）：
① $\text{[math]}$ 元
② $\text{[math]}$ 元
③ $\text{[math]}$ 元
过程探究3：一元一次方程问题设计，请你帮助解答：
1. （1）已知小菲家在2023年5月用电量为200千瓦时，且处于第一阶梯，她建议爸爸妈妈申请办理峰谷电，她说用峰谷电的话本月电费可以节约 $\text{[math]}$ 元，请问小菲家5月份用了多少千瓦时的峰电，多少千瓦时的谷电？
2. （2） 2023年10月份小华家用电量为180千瓦时，小菲家用电量为200千瓦时，在两家（小华家与小菲家）都不使用峰谷电的情况下，小华家的当月电费却超过了小菲家，请通过计算分析造成这种情况的原因．
3. （3）通过本项目的学习，你认为设置阶梯电价和峰谷电价的目的和意义是什么？
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

【培优卷】湘教版（2024）七年级上册3.7二元一次方程组的...

副标题：

*注意事项：

【培优卷】湘教版（2024）七年级上册3.7二元一次方程组的...

数学考试

试题分析

总体分析

题量分析

难度分析

知识点分析

	普通电价	峰时电价	谷时电价
第一阶梯：年用电量2760千瓦时及以下部分	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
第二阶梯：年用电量2761-4800千瓦时部分	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$
第三阶梯：年用电量4801千瓦时及以上部分	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

	甲	乙
成本（元/套）	20	24
售价（元/套）	25	30