浙江省嘉兴、舟山市2019年中考数学预测卷

更新时间：2024-07-13 浏览次数：510 类型：中考模拟

一、选择题（每小题3分，共30分）

1. (2019·嘉兴模拟) 左图所示物体的左视图是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2019七上·广陵月考) 钓鱼岛是我国固有领土，位于我国东海，总面积约6340000平方米，数据6340000用科学记数法表示为（）

A . 634×10⁴ B . 6.34×10⁶ C . 63.4×10⁵ D . 6.34×10⁷

答案解析收藏纠错 + 选题
3. (2019·嘉兴模拟) 如图，是某商场2013年至2017年销售额每年比上一年增长率的统计图，则这5年中，该商场销售额最大的是（）

A . 2017年 B . 2016年 C . 2015年 D . 2014年

答案解析收藏纠错 + 选题
4. (2018七下·马山期末) 如图，用不等式表示数轴上所示的解集，正确的是（）

A . x＞﹣2 B . x≥﹣2 C . x＜﹣2 D . x≤﹣2

答案解析收藏纠错 + 选题
5. (2019·嘉兴模拟) 如图，在长方形纸片ABCD中，AB=4，BC=6，将△ABC沿AC折叠，使点B落在点E处，CE交AD于点F，则DF的长等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2020九上·江阴月考) 若圆的半径是 $\text{[math]}$ ，圆心的坐标是 $\text{[math]}$ ，点 $\text{[math]}$ 的坐标是 $\text{[math]}$ ，则点 $\text{[math]}$ 与 $\text{[math]}$ 的位置关系是（）

A . 点P在⊙O外 B . 点P在⊙O内 C . 点P在⊙O上 D . 点P在⊙O外或⊙O上

答案解析收藏纠错 + 选题
7. (2019·嘉兴模拟) 如图，将图甲表示的正方形纸片剪成四块，恰好拼成图乙表示的矩形.若 $\text{[math]}$ ，则 $\text{[math]}$ 等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024九上·惠阳开学考) 如图， $\text{[math]}$ 为等腰三角形，如果把它沿底边 $\text{[math]}$ 翻折后，得到 $\text{[math]}$ ，那么四边形ABDC为（）

A . 一般平行四边形 B . 正方形 C . 矩形 D . 菱形

答案解析收藏纠错 + 选题
9. (2021·房县模拟) 如图，两个边长分别为a，b（a＞b）的正方形连在一起，三点C，B，F在同一直线上，反比例函数y= $\text{[math]}$ 在第一象限的图象经过小正方形右下顶点E．若OB²﹣BE²=10，则k的值是（）

A . 3 B . 4 C . 5 D . 4 $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2019·嘉兴模拟) 甲、乙、丙、丁四人分别面对面坐在一个四边形桌子旁边，桌上一张纸上写着数字“9”，甲说他看到的是“6”，乙说他看到的是“ ”，丙说他看到的是“ ”，丁说他看到的是“9”，则下列说法正确的是（）

A . 甲在丁的对面，乙在甲的左边，丙在丁的右边 B . 丙在乙的对面，丙的左边是甲，右边是乙 C . 甲在乙的对面，甲的右边是丙，左边是丁 D . 甲在丁的对面，乙在甲的右边，丙在丁的右边

答案解析收藏纠错 + 选题

二、填空题（每小题4分，共24分）

11. (2019·嘉兴模拟) 因式分解：3ax²+6ax+3a=．

答案解析收藏纠错 + 选题
12. (2022九上·昌平期中) 如图，AB∥CD∥EF，直线l₁、l₂分别与这三条平行线交于点A、C、E和点B、D、F．已知AC=3，CE=5，DF=4，则BF的长为．

答案解析收藏纠错 + 选题
13. (2019·嘉兴模拟) 三个筹码，第一个一面画上×，另一面画上○；第二个一面画上○，另一面画上#；第三个一面画上#，另一面画上×．甲、乙两人玩抛掷三个筹码的游戏，其游戏规则定为“掷出的三个筹码中　则甲方赢；否则，乙方赢”时，这个游戏是公平的．

答案解析收藏纠错 + 选题
14. (2020九上·南京期中) 如图，在⊙O中，直径EF⊥CD，垂足为M，若CD＝2，EM＝5，则⊙O的半径为.

答案解析收藏纠错 + 选题
15. (2019·嘉兴模拟) 某校师生到距离学校15千米的工地参加义务劳动，一部分人骑自行车，出发40分钟后，其余的人乘汽车出发，结果同时到达．已知汽车的速度是自行车的3倍，则骑自行车的人的速度是千米/时．

答案解析收藏纠错 + 选题
16. (2020九上·镇海期中) 如图，AB是半圆O的直径，E是弧BC的中点，OE交弦BC于点D.已知BC=8cm，DE=2cm，则AD的长为cm.

答案解析收藏纠错 + 选题

三、解答题（8小题，共66分）

17. (2019·嘉兴模拟) 计算：
1. （1） $\text{[math]}$ ；
2. （2）（1+ $\text{[math]}$ ）÷ $\text{[math]}$ ．
答案解析收藏纠错 + 选题
18. (2019七下·河南期末) 解下列方程（组）：
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
19. (2023七下·宣汉期末) 如图，在△ABC中，AB＝AC，D，E，F分别在三边上，且BE＝CD，BD＝CF，G为EF的中点．
1. （1）若∠A＝40°，求∠B的度数；
2. （2）试说明：DG垂直平分EF.
答案解析收藏纠错 + 选题
20. (2019·嘉兴模拟) 如图是根据对某区初中三个年级学生课外阅读的“漫画丛书”、“科普常识”、“名人传记”、“其它”中，最喜欢阅读的一种读物进行随机抽样调查，并绘制了下面不完整的条形统计图和扇形统计图（每人必选一种读物，并且只能选一种），根据提供的信息，解答下列问题：
1. （1）求该区抽样调查人数；
2. （2）补全条形统计图，并求出最喜欢“其它”读物的人数在扇形统计图中所占的圆心角度数；
3. （3）若该区有初中生14400人，估计该区有初中生最喜欢读“名人传记”的学生是多少人？
答案解析收藏纠错 + 选题

21. (2019·嘉兴模拟) 小明骑自行车去学校，最初以某一速度匀速行驶，中途自行车发生故障，停下来修车耽误了几分钟，为了按时到校，他加快了速度，仍保持匀速行驶，结果准时到校，到校后，小明画了自行车行进路程s(km)与行进时间t(h)的图象，如图所示，请回答：

（1）这个图象反映了哪两个变量之间的关系？

（2）根据图象填表：

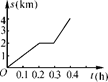
时间t/h	0	0.2	0.3	0.4
路程s/km

（3）路程s可以看成时间t的函数吗？

答案解析收藏纠错 + 选题

22. (2019·嘉兴模拟) 如图所示，点P表示广场上的一盏照明灯．
1. （1）请你在图中画出小敏在照明灯照射下的影子(用线段表示)；
2. （2）若小丽到灯柱MO的距离为4.5米，照明灯P到灯柱的距离为1.5米，小丽目测照明灯P的仰角为55°，她的目高QB为1.6米，试求照明灯P到地面的距离(结果精确到0.1米)．
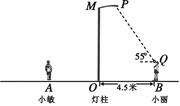
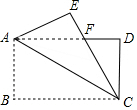
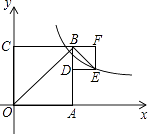
  (参考数据：tan55°≈1.428，sin55°≈0.819，cos55°≈0.574)
答案解析收藏纠错 + 选题
23. (2019·嘉兴模拟) 如图，抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴的交点为A、B，与 $\text{[math]}$ 轴的交点为C，顶点为 $\text{[math]}$ ，将抛物线 $\text{[math]}$ 绕点B旋转 $\text{[math]}$ ，得到新的抛物线 $\text{[math]}$ ，它的顶点为D.
1. （1）求抛物线 $\text{[math]}$ 的解析式；
2. （2）设抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴的另一个交点为E，点P是线段ED上一个动点（P不与E、D重合），过点P作y轴的垂线，垂足为F，连接EF.如果P点的坐标为 $\text{[math]}$ ，△PEF的面积为S，求S与 $\text{[math]}$ 的函数关系式，写出自变量 $\text{[math]}$ 的取值范围；
3. （3）设抛物线 $\text{[math]}$ 的对称轴与 $\text{[math]}$ 轴的交点为G，以G为圆心，A、B两点间的距离为直径作⊙G，试判断直线CM与⊙G的位置关系，并说明理由.
答案解析收藏纠错 + 选题
24. (2019·嘉兴模拟) 如图，在△ABC中，∠ACB=90°，CD是中线，AC=BC，一个以点D为顶点的45°角绕点D旋转，使角的两边分别与AC、BC的延长线相交，交点分别为E、F，DF与AC交于点M，DE与BC交于点N。
1. （1）求证：△ADM∽△BND；
2. （2）在∠EDF绕点D旋转的过程中：
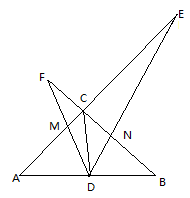
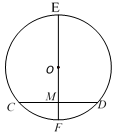
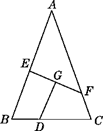
  ①探究三条线段CD、CE、CF之间的数量关系，并说明理由；
  
  ②若CE=4，CF=2，求DN的长.
答案解析收藏纠错 + 选题