17.
(2019·扬州)
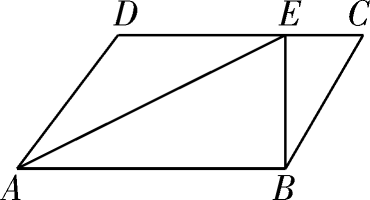
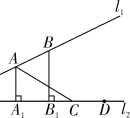
如图,在△ABC中,AB=5,AC=4,若进行一下操作,在边BC上从左到右一次取点D
1、D
2、D
3、D
4…;过点D1作AB、AC的平行线分别交于AC、AB与点E
1、F
1;过点D
2作AB、AC的平行线分别交于AC、AB于点E
2、F
2;过点D
3作AB、AC的平行线分别交于AC、AB于点E
3、F
3…,则4(D
1E
1+D
2E
2+…+D
2019E
2019)+5(D
1F
1+D
2F
2+…+D
2019F
2019)=
.

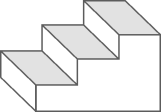
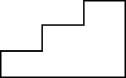 B .
B .  C .
C .  D .
D .