2017年河南省天宏大联考中考数学一模试卷

更新时间：2017-07-07 浏览次数：1417 类型：中考模拟

一、选择题

1. 在数﹣3，﹣2，0，3中，大小在﹣1和2之间的数是（　　）

A . ﹣3 B . ﹣2 C . 0 D . 3

答案解析收藏纠错 + 选题
2. 某同学画出了如图所示的几何体的三种视图，其中正确的是（）

A . ①② B . ①③ C . ②③ D . ②

答案解析收藏纠错 + 选题
3. 微信更具移动ID所带来的数据，发布了“微信用户春节迁徙数据报告”，该报告显示，2016年1月24日春运至2月4日期间，人口流入最多的省份是河南，作为劳务输出大省，河南约有313万微信用户在春节期间返乡，313万用科学记数法表示为（）

A . 3.13×10⁵ B . 3.13×10⁶ C . 3.13×10² D . 313×10⁴

答案解析收藏纠错 + 选题
4. 如图，在平行四边形ABCD中，EF∥AB交AD于E，交BD于F，DE：EA=3：4，EF=3，则CD的长为（）

A . 4 B . 7 C . 3 D . 12

答案解析收藏纠错 + 选题
5. 已知，一次函数y₁=ax+b与反比例函数y₂= $\text{[math]}$ 的图象如图所示，当y₁＜y₂时，x的取值范围是（）

A . x＜2 B . 0＜x＜2或x＞5 C . 2＜r＜5 D . r＞5

答案解析收藏纠错 + 选题
6. 已知边长为m的正方形面积为12，则下列关于m的说法中，错误的是（）
①m是无理数；
②m是方程m²﹣12=0的解；
③m满足不等式组 $\text{[math]}$ ；
④m是12的算术平方根．

A . ①② B . ①③ C . ③ D . ①②④

答案解析收藏纠错 + 选题
7. (2016·石峰模拟)
如图，挂在弹簧称上的长方体铁块浸没在水中，提着弹簧称匀速上移，直至铁块浮出水面停留在空中（不计空气阻力），弹簧称的读数F（N）与时间t（s）的函数图象大致是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
8.
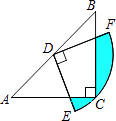
如图，在△ABC中，∠ACB=90°，分别以点A和点B为圆心，以相同的长（大于 $\text{[math]}$ AB）为半径作弧，两弧相交于点M和点N，作直线MN交AB于点D，交BC于点E．若AC=3，AB=5，则DE等于（　　）

A . 2 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9.
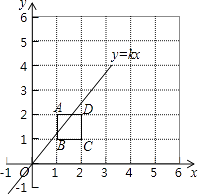
将2×2的正方形网格如图所示的放置在平面直角坐标系中，每个小正方形的顶点称为格点，每个小正方形的边长都是1，正方形ABCD的顶点都在格点上，若直线y=kx（k≠0）与正方形ABCD有公共点，则k不可能是（）

A . 3 B . 2 C . 1 D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. 在平面直角坐标系中，正方形A₁B₁C₁D₁、D₁ E₁E₂B₂、A₂B₂ C₂D₂、D₂E₃E4B₃…按如图所示的方式放置，其中点B₁在y轴上，点C₁、E₁、E₂、C₂、E₃、E₄、C₃…在x轴上，已知正方形A₁B₁C₁D₁的边长为l，∠B₁C₁O=60°，B₁C₁∥B₂C₂∥B₃C₃…，则正方形A₂₀₁₇B₂₀₁₇C₂₀₁₇ D₂₀₁₇的边长是（）

A . （ $\text{[math]}$ ）²⁰¹⁶ B . （ $\text{[math]}$ ）²⁰¹⁷ C . （ $\text{[math]}$ ）²⁰¹⁶ D . （ $\text{[math]}$ ）²⁰¹⁷

答案解析收藏纠错 + 选题

二、填空题

11. |﹣2|﹣（π﹣3）⁰=．

答案解析收藏纠错 + 选题
12. 用等腰直角三角板画∠AOB=45°，并将三角板沿OB方向平移到如图所示的虚线处后绕点M逆时针方向旋转22°，则三角板的斜边与射线OA的夹角α为度．

答案解析收藏纠错 + 选题
13. (2017·濮阳模拟) 一只昆虫在如图所示的树枝上寻觅食物，假定昆虫在每个岔路口都会随机选择一条路径，则它获取食物的概率是．

答案解析收藏纠错 + 选题
14. (2017·河北模拟) 如图，在△ABC中，CA=CB，∠ACB=90°，AB=2，点D为AB的中点，以点D为圆心作圆心角为90°的扇形DEF，点C恰在弧EF上，则图中阴影部分的面积为．

答案解析收藏纠错 + 选题
15. 如图，在Rt△ABC中，∠ACB=90°，AB=5，AC=3，点D是BC上一动点，连接AD，将△ACD沿AD折叠，点C落在点E处，连接DE交AB于点F，当△DEB是直角三角形时，DF的长为．

答案解析收藏纠错 + 选题

三、解答题

16. 先化简，再求值： $\text{[math]}$ ÷ $\text{[math]}$ ，其中m是方程x²+2x﹣3=0的根．

答案解析收藏纠错 + 选题
17. 中华文明，源远流长：中华汉字，寓意深广，为了传承优秀传统文化，某校团委组织了一次全校3000名学生参加的“汉字听写”大赛，赛后发现所有参赛学生的成绩均不低于50分．为了更好地了解本次大赛的成绩分布情况，随机抽取了其中200名学生的成绩（成绩x取整数，总分100分）作为样本进行整理，得到下列不完整的统计图表：
成绩x/分
频数
频率
50≤x＜60
10
0.05
60≤x＜70
20
0.10
70≤x＜80
30
b
80≤x＜90
a
0.30
90≤x≤100
80
0.40
请根据所给信息，解答下列问题：
1. （1） a=，b=；
2. （2）请补全频数分布直方图；
3. （3）这次比赛成绩的中位数会落在分数段；
4. （4）若成绩在90分以上（包括90分）的为“优”等，则该校参加这次比赛的3000名学生中成绩“优”等约有多少人？
答案解析收藏纠错 + 选题
18. 在Rt△ABC中，∠ACB=90°，以点A为圆心，AC为半径，作⊙A交AB于点D，交CA的延长线于点E，过点E作AB的平行线EF交⊙A于点F，连接AF、BF，DF．
1. （1）求证：BF⊥AF；
2. （2）当∠CAB等于多少度时，四边形ADEF为菱形？请给予证明．
答案解析收藏纠错 + 选题
19. 某中学广场上有旗杆如图1所示，在学习解直角三角形以后，数学兴趣小组测量了旗杆的高度．如图2，某一时刻，旗杆AB的影子一部分落在平台上，另一部分落在斜坡上，测得落在平台上的影长BC为4米，落在斜坡上的影长CD为3米，AB⊥BC，同一时刻，光线与水平面的夹角为72°，1米的竖立标杆PQ在斜坡上的影长QR为2米，求旗杆的高度（结果精确到0.1米）．（参考数据：sin72°≈0.95，cos72°≈0.31，tan72°≈3.08）

答案解析收藏纠错 + 选题
20.
某经销商销售一种产品，这种产品的成本价为10元/千克，市场调查发现，该产品每天的销售量y（千克）与销售价x（元/千克，且10≤x≤18）之间的函数关系如图所示；
1. （1）求y（千克）与销售价x的函数关系式；
2. （2）该经销商想要获得150元的销售利润，销售价应定为多少？
答案解析收藏纠错 + 选题
21. 有这样一个问题：探究函数 $\text{[math]}$ 的图象与性质．小怀根据学习函数的经验，对函数 $\text{[math]}$ 的图象与性质进行了探究．下面是小怀的探究过程，请补充完成：
1. （1）函数 $\text{[math]}$ 的自变量x的取值范围是；
2. （2）列出y与x的几组对应值．请直接写出m的值，m=；
3. （3）请在平面直角坐标系xOy中，描出以上表中各对对应值为坐标的点，并画出该函数的图象；
4. （4）结合函数的图象，写出函数 $\text{[math]}$ 的一条性质．
  x
  …
  ﹣5
  ﹣4
  ﹣3
  ﹣2
  ﹣ $\text{[math]}$
  ﹣ $\text{[math]}$
  0
  1
  2
  m
  4
  5
  …
  y
  …
     $\text{[math]}$
     $\text{[math]}$
     $\text{[math]}$
  2
  3
  ﹣1
  0
     $\text{[math]}$
     $\text{[math]}$
     $\text{[math]}$
     $\text{[math]}$
     $\text{[math]}$
  …
答案解析收藏纠错 + 选题
22.
我们把两条中线互相垂直的三角形称为“中垂三角形”，例如图1，图2，图3中，AF，BE是△ABC的中线，AF⊥BE，垂足为P，像△ABC这样的三角形均为“中垂三角形”，设BC=a，AC=b，AB=c．
1. （1）【特例探索】
  如图1，当∠ABE=45°，c=2 $\text{[math]}$ 时，a=，b=；如图2，当∠ABE=30°，c=4时，a=，b=；
2. （2）【归纳证明】
  
  请你观察（1）中的计算结果，猜想a² ， b² ， c²三者之间的关系，用等式表示出来，请利用图3证明你发现的关系式；
3. （3）
  【拓展应用】
  
  如图4，在▱ABCD中，点E，F，G分别是AD，BC，CD的中点，BE⊥EG，AD=2 $\text{[math]}$ ，AB=3．求AF的长．
答案解析收藏纠错 + 选题
23.
如图，抛物线y= $\text{[math]}$ x²+bx+c与y轴交于点C（0，﹣4），与x轴交于点A、B，且B点的坐标为（2，0）．
1. （1）求抛物线的解析式；
2. （2）若点P是AB上的一个动点，过点P作PE∥AC交BC于点E，连接CP，求△PCE面积最大时P点的坐标；
3. （3）在（2）的条件下，若点D为OA的中点，点M是线段AC上一点，当△OMD为等腰三角形时，连接MP、ME，把△MPE沿着PE翻折，点M的对应点为点N，直接写出点N的坐标．
答案解析收藏纠错 + 选题