图1所示是太极图,俗称“阴阳鱼”,该图案关于外圈大圆的圆心中心对称;
图2所示是一个正三角形内接于圆;
图3所示是一个正方形内接于圆;
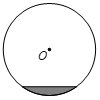
图4所示是两个同心圆,其中小圆的半径是外圈大圆半径的三分之二.
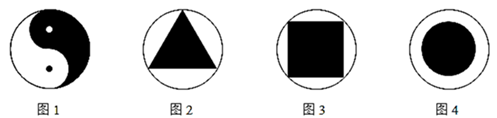
这四个图案中,阴影部分的面积不小于该图案外圈大圆面积一半的是( )
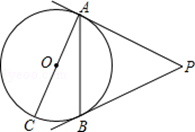


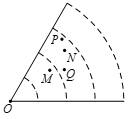
⑴作AB和BC的垂直平分线交于点O;
⑵以点O为圆心,OA长为半径作圆;
⑶⊙O分别与AB和BC的垂直平分线交于点M,N;
⑷连接AM,AN,CM,其中AN与CM交于点P.
根据以上作图过程及所作图形,下列四个结论中,
① ; ②
;
③点O是 的外心 ; ④点P是
的内心.
所有正确结论的序号是.


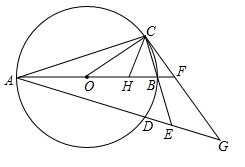
①求证:△CBH∽△OBC;
②求OH+HC的最大值.
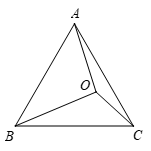
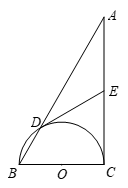


图2
|
x |
… |
| | 0 | | 2 | | 3 | … |
| y | … | | | 0 | m | n | | 3 | … |
请直接写出:m=,n=;
② 若 ,结合函数图象,直接写出b的取值范围.

备用图

①如图2,C是直线l上的一个动点,若C是线段AB的直角点,求点C的坐标;

②如图3,P是直线l上的一个动点,将所有线段AP的等腰直角点称为直线l关于点A的伴随点.若⊙O的半径为r,且⊙O上恰有两个点为直线l关于点A的伴随点,直接写出r的取值范围.
