

甲同学:A(0,1),B(0,0),C(1,0),D(1,1);
乙同学:A(0,0),B(0,﹣1),C(1,﹣1),D(1,0);
丙同学:A(1,0),B(1,﹣2),C(3,﹣2),D(3,0);
丁同学:A(﹣1,2),B(﹣1,0),C(0,0),D(0,2);
上述四名同学表示的结果中,四个点的坐标都表示正确同学是( )




已知:△ABC.
求作:BC边上的高线.
作法:如图2,
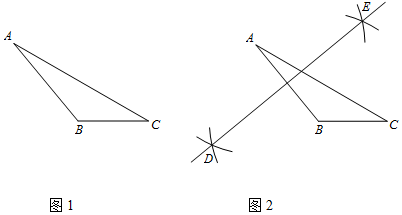
①分别以A,B为圆心,大于 AB长为半径画弧,两弧交于点D,E;
②作直线DE,与AB交于点F,以点F为圆心,FA长为半径画圆,交CB的延长线于点G;
③连接AG.
所以线段AG就是所求作的BC边上的高线.
根据小明设计的尺规作图过程,
证明:连接DA,DB,EA,EB,
∵DA=DB,
∴点D在线段AB的垂直平分线上()(填推理的依据).
∵=,
∴点E在线段AB的垂直平分线上.
∴DE是线段AB的垂直平分线.
∴FA=FB.
∴AB是⊙F的直径.
∴∠AGB=90°()(填推理的依据).
∴AG⊥BC
即AG就是BC边上的高线.

①当m=4时,直接写出区域W内的整点个数;
②若区域W内的整点个数不超过8个,结合图象,求m的取值范围.
①A、B两班学生(两个班的人数相同)数学成绩不完整的频数分布直方图如下(数据分成5组:x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100):
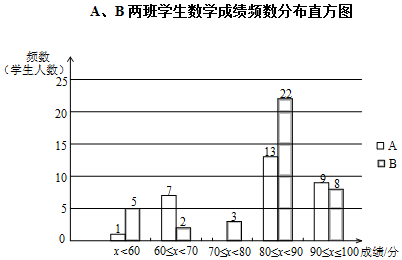
②A、B两班学生测试成绩在80≤x<90这一组的数据如下:
A班:80 80 82 83 85 85 86 87 87 87 88 89 89
B班:80 80 81 81 82 82 83 84 84 85 85 86 86 86 87 87 87 87 87 88 88 89
③A、B两班学生测试成绩的平均数、中位数、方差如下:
| 平均数 | 中位数 | 方差 | |
| A班 | 80.6 | m | 96.9 |
| B班 | 80.8 | n | 153.3 |
根据以上信息,回答下列问题:

小东根据学习函数的经验,分别对函数y1、y2随自变量x的变化而变化的规律进行了探究:
下面是小东的探究过程,请补充完整:
|
x/cm |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
y1/cm |
0 |
2.45 |
3.46 |
4.90 |
5.48 |
6 |
|
|
y2/cm |
4 |
3.74 |
3.46 |
3.16 |
2.83 |
2.45 |
2 |

①当AC>CM时,线段AP的取值范围是;
②当△AMC是等腰三角形时,线段AP的长约为.
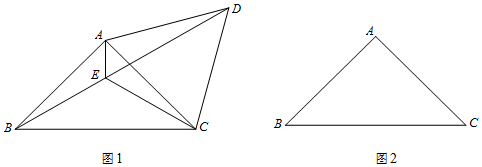
连结CE.
①求证:∠AED=∠CED;
②用等式表示线段AE、CE、BD之间的数量关系(直接写出结果);

例如:若点M(﹣1,1),点N (2,﹣2),则点M与点N的“折线距离”为:d(M,N)=|﹣1﹣2|+|1﹣(﹣2)|=3+3=6.
根据以上定义,解决下列问题:
①若点A(﹣2,﹣1),则d(P,A)=;
②若点B(b,2),且d(P,B)=5,则b=;