四川省乐山市井研县2019年中考数学5月模拟考试试卷

更新时间：2020-05-15 浏览次数：175 类型：中考模拟

一、选择题

1. (2020·武汉模拟) 有理数－2的绝对值是（）

A . 2 B . －2 C . － $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2019·井研模拟) 下列运算正确的是（）

A . 2x+3y=5xy B . （x+3）²=x²+9 C . （xy²）³=x³y⁶ D . x¹⁰÷x⁵=x²

答案解析收藏纠错 + 选题
3. (2020七下·北海期末) 如图，直线l₁∥l₂ ，且分别与直线l交于C，D两点，把一块含30°角的三角尺按如图所示的位置摆放.若∠1=52°，则∠2的度数为（）

A . 92° B . 98° C . 102° D . 108°

答案解析收藏纠错 + 选题
4. (2019·井研模拟) 下列说法正确的是（）

A . 了解“乐山市初中生每天课外阅读书籍时间的情况”最适合的调查方式是全面调查 B . 甲乙两人跳绳各10次，其成绩的平均数相等， $\text{[math]}$ ，则甲的成绩比乙稳定 C . 一口袋中装有除颜色外其余均相同的红色小球2个，蓝色小球1个，从中随机一次性摸出2个小球，则恰好摸到同色小球的概率是 $\text{[math]}$ D . “任意画一个三角形，其内角和是360°”这一事件是不可能事件

答案解析收藏纠错 + 选题
5. (2024九下·莆田月考) 我国古代数学著作《九章算术》卷七有下列问题：“今有共买物，人出八，盈三：人出七，不足四，问人数、物价几何？”意思是：现在有几个人共同出钱去买件物品，如果每人出8钱，则剩余3钱：如果每人出7钱，则差4钱．问有多少人，物品的价格是多少？设有x人，物品的价格为y元，可列方程（组）为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$ = $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2019·井研模拟) 已知关于x的不等式组 $\text{[math]}$ 只有2个整数解，则m的取值范围为（）

A . m＞4 B . 4＜m＜5 C . 4≤m＜5 D . 4＜m≤5

答案解析收藏纠错 + 选题
7. (2023·雷州模拟) 下列图形中既是轴对称图形又是中心对称图形的是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
8. (2020九上·曲阳期末) 如图，将△ABC沿BC边上的中线AD平移到△A'B'C'的位置，已知△ABC的面积为9，阴影部分三角形的面积为4.若AA'=1，则A'D等于（）

A . 2 B . 3 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2021·恩施模拟) 二次函数y＝ax²+bx+c（a≠0）的大致图象如图所示，顶点坐标为（﹣2，﹣9a），下列结论：①abc＜0；②4a+2b+c＞0；③5a﹣b+c＝0；④若方程a（x+5）（x﹣1）＝﹣1有两个根x₁和x₂ ，且x₁＜x₂ ，则﹣5＜x₁＜x₂＜1；⑤若方程|ax²+bx+c|＝1有四个根，则这四个根的和为﹣8，其中正确的结论有（）

A . ①②③④ B . ①②③⑤ C . ②③④⑤ D . ①②④⑤

答案解析收藏纠错 + 选题
10. (2019·井研模拟) 如图，菱形ABCD的边AD⊥y轴，垂足为点E，顶点A在第二象限，顶点B在y轴的正半轴上，反比例函数y= $\text{[math]}$ （k≠0，x＞0）的图象同时经过顶点C，D．若点C的横坐标为5，BE=3DE，则k的值为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 3 D . 5

答案解析收藏纠错 + 选题

二、填空题

11. (2024八下·汕尾期末) 如果二次根式 $\text{[math]}$ 有意义，那么x的取值范围是．

答案解析收藏纠错 + 选题
12. (2020七上·武进月考) 地球与月球的平均距离大约384000km，用科学记数法表示这个距离为km.

答案解析收藏纠错 + 选题
13. (2024八下·锦江期末) 分解因式： $\text{[math]}$ =

答案解析收藏纠错 + 选题
14. (2019·井研模拟) 如图，从一块直径为2m的圆形铁皮上剪出一个圆心角为90°的扇形（阴影部分），则此扇形的面积为m² ．

答案解析收藏纠错 + 选题
15. (2020九下·长沙开学考) 如图，圆锥侧面展开得到扇形，此扇形半径 CA=6，圆心角∠ACB=120°，则此圆锥高 OC 的长度是．

答案解析收藏纠错 + 选题
16. (2019·井研模拟) 阅读：我们约定，在平面直角坐标系中，经过某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线，叫该点的“特征线”。例如，点M(1，3)的特征线有：x=1，y=3，y=x+2，y=−x+4.如图，在平面直角坐标系中有正方形OABC，点B在第一象限，A、C分别在x轴和y轴上，抛物线 $\text{[math]}$ 经过B. C两点，顶点D在正方形内部。
1. （1）写出点M（2，3）任意两条特征线
2. （2）若点D有一条特征线是y=x+1，求此抛物线的解析式
答案解析收藏纠错 + 选题

三、计算题

17. (2020·珠海模拟) 计算： $\text{[math]}$ +（ $\text{[math]}$ ）⁰+ $\text{[math]}$ •sin45°﹣（π﹣2019）⁰ ．

答案解析收藏纠错 + 选题
18. (2019·井研模拟) 先化简，再求值： $\text{[math]}$ ，其中x的值是方程x²+2x＝0的根．

答案解析收藏纠错 + 选题

四、综合题

19. (2019·井研模拟) 如图，在△ABC中，D是BC边上的一点，E是AD的中点，过点A作BC的平行线交CE的延长线于点F ，且AF＝BD ，连接BF ．
1. （1）求证：D是BC的中点；
2. （2）若BA⊥AC ，试判断四边形AFBD的形状，并证明你的结论．
答案解析收藏纠错 + 选题
20. (2019·井研模拟) 为调查我市民上班时最常用的交通工具的情况随机抽取了部分市民进行调查，要求被调查者从“A：自行车，B：电动车，C：公交车，D：家庭汽车；E ．其他”中选择最常用的一项．将所有调查结果整理后绘制成如下不完整计图，请结合统计图回答下列问题：
1. （1）本次一共调查了名市民；扇形统计图中B项对应的圆心角是度；
2. （2）补全条形统计图；
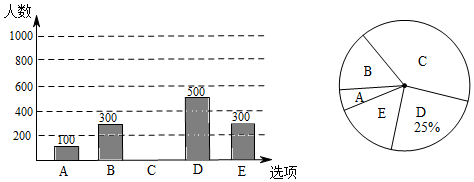
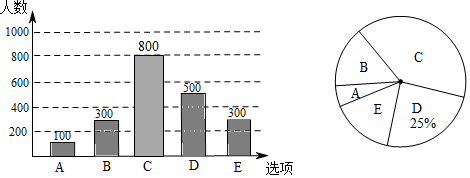3. （3）若甲、乙两人上班时从A、B、C、D四种交通工具中随或画树状图的方法，求出甲、乙两人恰好选择同一种交通工具上班的概率．
答案解析收藏纠错 + 选题
21. (2021·黄石模拟) 已知关于x的一元二次方程x²+（2m+1）x+m²﹣2=0．
1. （1）若该方程有两个实数根，求m的最小整数值；
2. （2）若方程的两个实数根为x₁ ， x₂ ，且（x₁﹣x₂）²+m²=21，求m的值．
答案解析收藏纠错 + 选题
22. (2019·井研模拟) 某游乐场一转角滑梯如图所示，滑梯立柱AB、CD均垂直于地面，点E在水平地面上BD上，在C点测得点A的仰角为30°，斜面EC的坡度为1： $\text{[math]}$ ，测得B、E间距离为10米，立柱AB高30米，求立柱CD的高（结果保留根号）．

答案解析收藏纠错 + 选题
23. (2019·井研模拟) 如图，反比例函数y＝ $\text{[math]}$ （k≠0）的图象与正比例函数y＝2x的图象相交于A（1，a）、B两点，点C在第四象限，CA∥y轴，且CB⊥AB ．
1. （1）求反比例函数的解析式及点B的坐标；
2. （2）求tanC的值和△ABC的面积．
答案解析收藏纠错 + 选题
24. (2019·井研模拟) 如图所示，AB是⊙O的直径，G为弦AE的中点，OG的延长线交⊙O于点D ，连接BD交AE于点F ，延长AE至点C ，使得FC＝BC ，连接BC ．
1. （1）求证：BC是⊙O的切线；
2. （2） ⊙O的半径为10，tanA＝ $\text{[math]}$ ，求BF的长．
答案解析收藏纠错 + 选题
25. (2019·井研模拟) 阅读材料：各类方程的解法
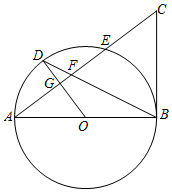
求解一元一次方程，根据等式的基本性质，把方程转化为x=a的形式．求解二元一次方程组，把它转化为一元一次方程来解；类似的，求解三元一次方程组，把它转化为解二元一次方程组．求解一元二次方程，把它转化为两个一元一次方程来解．求解分式方程，把它转化为整式方程来解，由于“去分母”可能产生增根，所以解分式方程必须检验．各类方程的解法不尽相同，但是它们有一个共同的基本数学思想 $\text{[math]}$ 转化，把未知转化为已知．

用“转化”的数学思想，我们还可以解一些新的方程．例如，一元三次方程x³+x²-2x=0，可以通过因式分解把它转化为x(x²+x-2)=0，解方程x=0和x²+x-2=0，可得方程x³+x²-2x=0的解．
1. （1）问题：方程x³+x²-2x=0的解是x₁=0，x₂=，x₃=；
2. （2）拓展：用“转化”思想求方程 $\text{[math]}$ 的解；
3. （3）应用：如图，已知矩形草坪ABCD的长AD=8m，宽AB=3m，小华把一根长为10m的绳子的一端固定在点B，沿草坪边沿BA，AD走到点P处，把长绳PB段拉直并固定在点P，然后沿草坪边沿PD、DC走到点C处，把长绳剩下的一段拉直，长绳的另一端恰好落在点C．求AP的长．
答案解析收藏纠错 + 选题
26. (2019·井研模拟) 如图1，已知抛物线y=﹣x²+bx+c与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于C点，点P是抛物线上在第一象限内的一个动点，且点P的横坐标为t．
1. （1）求抛物线的表达式；
2. （2）设抛物线的对称轴为l，l与x轴的交点为D．在直线l上是否存在点M，使得四边形CDPM是平行四边形？若存在，求出点M的坐标；若不存在，请说明理由．
3. （3）如图2，连接BC，PB，PC，设△PBC的面积为S．
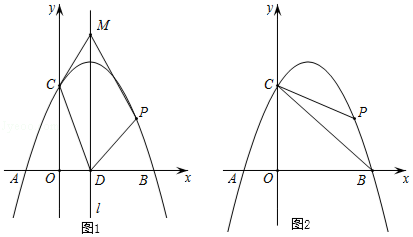
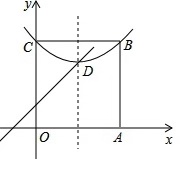
  ①求S关于t的函数表达式；
  ②求P点到直线BC的距离的最大值，并求出此时点P的坐标．
答案解析收藏纠错 + 选题