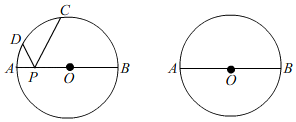
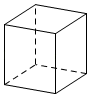
 B .
B . 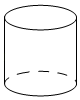 C .
C . 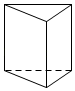 D .
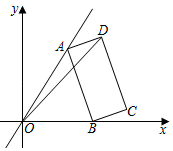
D . 

|
组别 |
次数x |
频数(人数) |
|
第1组 |
80≤x<100 |
6 |
|
第2组 |
100≤x<120 |
8 |
|
第3组 |
120≤x<140 |
12 |
|
第4组 |
140≤x<160 |
a |
|
第5组 |
160≤x<180 |
6 |

请结合图表完成下列问题: