



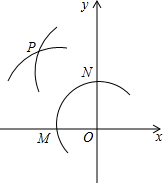

抽签规则:将4名女班干部姓名分别写在4张完全相同的卡片正面,把四张卡片背面朝上,洗匀后放在桌面上,梁老师先从中随机抽取一张卡片,记下姓名,再从剩余的3张卡片中随机抽取第二张,记下姓名.
莱昂哈德·欧拉(LeonhardEuler)是瑞士数学家,在数学上经常见到以他的名字命名的重要常数、公式和定理,下面是欧拉发现的一个定理:在△ABC中,R和r分别为外接圆和内切圆的半径,O和I分别为其外心和内心,则OI =R
-2Rr.
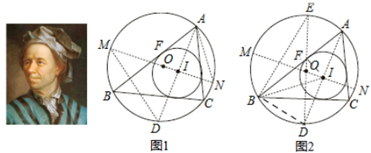
下面是该定理的证明过程(借助了第(2)问的结论):
延长AI交⊙O于点D,过点I作⊙O的直径MN,连接DM,AN.
∵∠D=∠N,∴∠DMI=∠NAI(同弧所对的圆周角相等),
∴△MDI∽△ANI.∴ ,∴IA×ID=IM×IN①
如图②,在图1(隐去MD,AN)的基础上作⊙O的直径DE,连接BE,BD,BI,IF
∵DE是⊙O的直径,∴∠DBE=90°.
∵⊙I与AB相切于点F,∴∠AFI=90°,
∴∠DBE=∠IFA.
∵∠BAD=∠E(同弧所对圆周角相等),
∴△AIF∽△EDB.
∴ ,∴
②,
由(2)知: ,
∴
又∵ ,
∴2Rr=(R+d)(R-d),
∴R -d
=2Rr
∴d =R
-2Rr
任务:

如果函数y=f(x)满足:对于自变量x的取值范围内的任意x1 , x2 ,
①若x1<x2 , 都有f(x1)<f(x2),则称f(x)是增函数;
②若x1<x2 , 都有f(x1)>f(x2),则称f(x)是减函数.
例题:证明函数f(x)= (x>0)是减函数.
证明:设0<x1<x2 ,
f(x1)﹣f(x2)= .
∵0<x1<x2 ,
∴x2﹣x1>0,x1x2>0.
∴ >0.即f(x1)﹣f(x2)>0.
∴f(x1)>f(x2).
∴函数f(x)= (x>0)是减函数.
根据以上材料,解答下面的问题:
已知函数 .
f(﹣1)= +(﹣2)=-1,f(﹣2)=
+(﹣4)=
.




特例验证:
猜想论证:
拓展应用:
例如:如图1,点P在△ABC的内部,∠PBC=∠A,∠PCB=∠ABC,则△BCP∽△ABC,故点P为△ABC的自相似点.
请你运用所学知识,结合上述材料,解决下列问题:
在平面直角坐标系中,点M是曲线C: 上的任意一点,点N是x轴正半轴上的任意一点.
