北京市2020年中考数学试卷

更新时间：2020-08-06 浏览次数：861 类型：中考真卷

一、单选题

1. (2023·北京市模拟) 如图是某几何体的三视图，该几何体是（）

A . 圆柱 B . 圆锥 C . 三棱锥 D . 长方体

答案解析收藏纠错 + 选题
2. (2024九下·昂仁模拟) 2020年6月23日，北斗三号最后一颗全球组网卫星从西昌发射中心发射升空，6月30日成功定点于距离地球36000公里的地球同步轨道．将36000用科学记数法表示应为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2020·北京) 如图，AB和CD相交于点O，则下列结论正确的是（）

A . ∠1=∠2 B . ∠2=∠3 C . ∠1＞∠4+∠5 D . ∠2＜∠5

答案解析收藏纠错 + 选题
4. (2020·北京) 下列图形中，既是中心对称图形也是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
5. (2023八上·北京市开学考) 正五边形的外角和为（）

A . 180° B . 360° C . 540° D . 720°

答案解析收藏纠错 + 选题
6. (2023·南山模拟) 实数a在数轴上的对应点的位置如图所示．若实数 $\text{[math]}$ 满足 $\text{[math]}$ ，则b的值可以是（）

A . 2 B . -1 C . -2 D . -3

答案解析收藏纠错 + 选题
7. (2024九下·肇源模拟) 不透明的袋子中装有两个小球，上面分别写着“1”，“2”，除数字外两个小球无其他差别．从中随机摸出一个小球，记录其数字，放回并摇匀，再从中随机摸出一个小球，记录其数字，那么两次记录的数字之和为3的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024九上·婺城期末) 有一个装有水的容器，如图所示．容器内的水面高度是10cm，现向容器内注水，并同时开始计时，在注水过程中，水面高度以每秒0.2cm的速度匀速增加，则容器注满水之前，容器内的水面高度与对应的注水时间满足的函数关系是（）

A . 正比例函数关系 B . 一次函数关系 C . 二次函数关系 D . 反比例函数关系

答案解析收藏纠错 + 选题

二、填空题

9. (2024九下·靖江模拟) 若代数式 $\text{[math]}$ 有意义，则实数x的取值范围是．

答案解析收藏纠错 + 选题
10. (2024九上·北京市开学考) 已知关于 $\text{[math]}$ 的方程 $\text{[math]}$ 有两个相等的实数根，则k的值是．

答案解析收藏纠错 + 选题
11. (2023九上·淮阳期中) 写出一个比 $\text{[math]}$ 大且比 $\text{[math]}$ 小的整数．

答案解析收藏纠错 + 选题
12. (2024九下·昂仁模拟) 方程组 $\text{[math]}$ 的解为．

答案解析收藏纠错 + 选题
13. (2024九下·房山模拟) 在平面直角坐标系 $\text{[math]}$ 中，直线 $\text{[math]}$ 与双曲线 $\text{[math]}$ 交于A，B两点．若点A，B的纵坐标分别为 $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
14. (2021八下·澄海期末) 在 $\text{[math]}$ ABC中，AB=AC，点D在BC上（不与点B，C重合）．只需添加一个条件即可证明 $\text{[math]}$ ABD≌ $\text{[math]}$ ACD，这个条件可以是（写出一个即可）

答案解析收藏纠错 + 选题
15. (2021七下·历城期中) 如图所示的网格是正方形网格，A，B，C，D是网格交点，则 $\text{[math]}$ ABC的面积与 $\text{[math]}$ ABD的面积的大小关系为： $\text{[math]}$ $\text{[math]}$ （填“＞”，“＝”或“＜”）

答案解析收藏纠错 + 选题
16. (2020九上·北京月考) 如图是某剧场第一排座位分布图：甲、乙、丙、丁四人购票，所购票分别为2，3，4，5．每人选座购票时，只购买第一排的座位相邻的票，同时使自己所选的座位之和最小．如果按“甲、乙、丙、丁”的先后顺序购票，那么甲甲购买1，2号座位的票，乙购买3，5，7号座位的票，丙选座购票后，丁无法购买到第一排座位的票．若丙第一购票，要使其他三人都能购买到第一排座位的票，写出一种满足条件的购票的先后顺序．

答案解析收藏纠错 + 选题

三、解答题

17. (2024九下·常州模拟) 计算： $\text{[math]}$

答案解析收藏纠错 + 选题
18. (2022九下·南平期中) 解不等式组： $\text{[math]}$

答案解析收藏纠错 + 选题
19. (2024八上·双辽期末) 已知 $\text{[math]}$ ，求代数式 $\text{[math]}$ 的值．

答案解析收藏纠错 + 选题
20. (2020·北京) 已知：如图， $\text{[math]}$ ABC为锐角三角形，AB=BC，CD∥AB．
求作：线段BP，使得点P在直线CD上，且∠ABP= $\text{[math]}$ ．

作法：①以点A为圆心，AC长为半径画圆，交直线CD于C，P两点；②连接BP．线段BP就是所求作线段．
1. （1）使用直尺和圆规，依作法补全图形（保留作图痕迹）
2. （2）完成下面的证明．
  证明：∵CD∥AB，
  
  ∴∠ABP=．
  
  ∵AB=AC，
  
  ∴点B在⊙A上．
  
  又∵∠BPC= $\text{[math]}$ ∠BAC（）（填推理依据）
  
  ∴∠ABP= $\text{[math]}$ ∠BAC
答案解析收藏纠错 + 选题
21. 如图，菱形ABCD的对角线AC，BD相交于点O，E是AD的中点，点F，G在AB上，EF⊥AB，OG∥EF．
1. （1）求证：四边形OEFG是矩形；
2. （2）若AD=10，EF=4，求OE和BG的长．
答案解析收藏纠错 + 选题
22. (2023九上·丰台期中) 在平面直角坐标系 $\text{[math]}$ 中，一次函数 $\text{[math]}$ 的图象由函数 $\text{[math]}$ 的图象平移得到，且经过点(1，2)．
1. （1）求这个一次函数的解析式；
2. （2）当 $\text{[math]}$ 时，对于 $\text{[math]}$ 的每一个值，函数 $\text{[math]}$ 的值大于一次函数 $\text{[math]}$ 的值，直接写出 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
23. (2021·杭州模拟) 如图，AB为⊙O的直径，C为BA延长线上一点，CD是⊙O的切线，D为切点，OF⊥AD于点E，交CD于点F．
1. （1）求证：∠ADC=∠AOF；
2. （2）若sinC= $\text{[math]}$ ，BD=8，求EF的长．
答案解析收藏纠错 + 选题
24. (2021·驻马店模拟) 小云在学习过程中遇到一个函数 $\text{[math]}$ ．下面是小云对其探究的过程，请补充完整：
1. （1）当 $\text{[math]}$ 时，对于函数 $\text{[math]}$ ，即 $\text{[math]}$ ，当 $\text{[math]}$ 时， $\text{[math]}$ 随x的增大而，且 $\text{[math]}$ ；对于函数 $\text{[math]}$ ，当 $\text{[math]}$ 时， $\text{[math]}$ 随x的增大而，且 $\text{[math]}$ ；结合上述分析，进一步探究发现，对于函数 $\text{[math]}$ ，当 $\text{[math]}$ 时，y随x的增大而．
2. （2）当 $\text{[math]}$ 时，对于函数 $\text{[math]}$ ，当 $\text{[math]}$ 时，y与x的几组对应值如下表：
  
  x
  
  0
  
  $\text{[math]}$
  
  1
  
  $\text{[math]}$
  
  2
  
  $\text{[math]}$
  
  3
  
  $\text{[math]}$
  
  y
  
  0
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  1
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
  
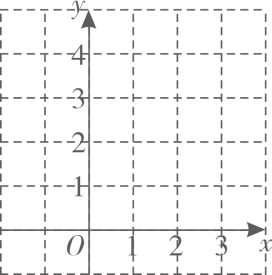
  综合上表，进一步探究发现，当 $\text{[math]}$ 时，y随x的增大而增大．在平面直角坐标系 $\text{[math]}$ 中，画出当 $\text{[math]}$ 时的函数y的图象．
3. （3）过点(0，m)（ $\text{[math]}$ ）作平行于x轴的直线l，结合（1）（2）的分析，解决问题：若直线l与函数 $\text{[math]}$ 的图象有两个交点，则m的最大值是．
答案解析收藏纠错 + 选题
25. (2022·烟台模拟) 小云统计了自己所住小区5月1日至30日的厨余垃圾分出量（单位：千克），相关信息如下：
a．小云所住小区5月1日至30日的厨余垃圾分出量统计图：

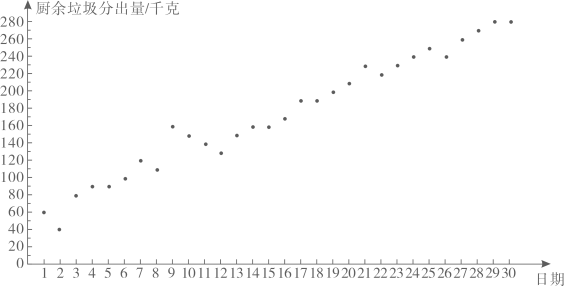
b．小云所住小区5月1日至30日分时段的厨余垃圾分出量的平均数如下：

时段

1日至10日

11日至20日

21日至30日

平均数

100

170

250
1. （1）该小区5月1日至30日的厨余垃圾分出量的平均数约为（结果取整数）
2. （2）已知该小区4月的厨余垃圾分出量的平均数为60，则该小区5月1日至30日的厨余垃圾分出量的平均数约为4月的倍（结果保留小数点后一位）；
3. （3）记该小区5月1日至10日的厨余垃圾分出量的方差为 $\text{[math]}$ 5月11日至20日的厨余垃圾分出量的方差为 $\text{[math]}$ ，5月21日至30日的厨余垃圾分出量的方差为 $\text{[math]}$ ．直接写出 $\text{[math]}$ 的大小关系．
答案解析收藏纠错 + 选题
26. (2020·北京) 在平面直角坐标系 $\text{[math]}$ 中， $\text{[math]}$ 为抛物线 $\text{[math]}$ 上任意两点，其中 $\text{[math]}$ ．
1. （1）若抛物线的对称轴为 $\text{[math]}$ ，当 $\text{[math]}$ 为何值时， $\text{[math]}$
2. （2）设抛物线的对称轴为 $\text{[math]}$ ．若对于 $\text{[math]}$ ，都有 $\text{[math]}$ ，求t的取值范围．
答案解析收藏纠错 + 选题
27. (2020·北京) 在 $\text{[math]}$ 中，∠C=90°，AC＞BC，D是AB的中点．E为直线上一动点，连接DE，过点D作DF⊥DE，交直线BC于点F，连接EF．
1. （1）如图1，当E是线段AC的中点时，设 $\text{[math]}$ ，求EF的长（用含 $\text{[math]}$ 的式子表示）；
2. （2）当点E在线段CA的延长线上时，依题意补全图2，用等式表示线段AE，EF，BF之间的数量关系，并证明．
答案解析收藏纠错 + 选题
28. (2020·北京) 在平面直角坐标系 $\text{[math]}$ 中，⊙O的半径为1，A，B为⊙O外两点，AB=1．给出如下定义：平移线段AB，得到⊙O的弦 $\text{[math]}$ （ $\text{[math]}$ 分别为点A，B的对应点），线段 $\text{[math]}$ 长度的最小值称为线段AB到⊙O的“平移距离”．
1. （1）如图，平移线段AB到⊙O的长度为1的弦 $\text{[math]}$ 和 $\text{[math]}$ ，则这两条弦的位置关系是；在点 $\text{[math]}$ 中，连接点A与点的线段的长度等于线段AB到⊙O的“平移距离”；
2. （2）若点A，B都在直线 $\text{[math]}$ 上，记线段AB到⊙O的“平移距离”为 $\text{[math]}$ ，求 $\text{[math]}$ 的最小值；
3. （3）若点A的坐标为 $\text{[math]}$ ，记线段AB到⊙O的“平移距离”为 $\text{[math]}$ ，直接写出 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

北京市2020年中考数学试卷

副标题：

*注意事项：

北京市2020年中考数学试卷

试题分析

总体分析

题量分析

难度分析

知识点分析

x	0	$\text{[math]}$	1	$\text{[math]}$	2	$\text{[math]}$	3	$\text{[math]}$
y	0	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	1	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$

时段	1日至10日	11日至20日	21日至30日
平均数	100	170	250