河南省驻马店市、天宏2021年数学中考一模大联考试卷

更新时间：2024-07-13 浏览次数：234 类型：中考模拟

一、单选题

1. (2022·长垣模拟) 下列各数中比 $\text{[math]}$ 小的数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024·南山模拟) 如图所示的圆锥，下列说法正确的是（）

A . 该圆锥的主视图是轴对称图形 B . 该圆锥的主视图是中心对称图形 C . 该圆锥的主视图既是轴对称图形，又是中心对称图形 D . 该圆锥的主视图既不是轴对称图形，又不是中心对称图形

答案解析收藏纠错 + 选题
3. (2021·路北模拟) 一只蚂蚁在如图所示的树枝上寻觅食物，假定蚂蚁在每个岔路口都随机选择一条路径，则它获得食物的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2021·驻马店模拟) 2020年6月23日，中国第55颗北斗导航卫星成功发射，顺利完成全球组网，其中支持北斗三号新信号的22纳米工艺射频基带一体化导航定位芯片，己实现规模化应用.22纳米 $\text{[math]}$ 米，将0.000000022用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2021·驻马店模拟) 如图，从笔直的公路 $\text{[math]}$ 旁一点P出发，向西走 $\text{[math]}$ 到达 $\text{[math]}$ ；从P出发向北走 $\text{[math]}$ 也到达l．下列说法错误的是（）

A . 从点P向北偏西45°走 $\text{[math]}$ 到达l B . 公路l的走向是南偏西45° C . 公路l的走向是北偏东45° D . 从点P向北走 $\text{[math]}$ 后，再向西走 $\text{[math]}$ 到达l

答案解析收藏纠错 + 选题
6. (2021八下·东阳期末) 如图，函数 $\text{[math]}$ 与函数 $\text{[math]}$ 的图象相交于点 $\text{[math]}$ .若 $\text{[math]}$ ，则x的取值范围是（）

A . $\text{[math]}$ 或 $\text{[math]}$ B . $\text{[math]}$ 或 $\text{[math]}$ C . $\text{[math]}$ 或 $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2020七上·滕州期末) 根据图中给出的信息，可得正确的方程是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2022·威海模拟) 如图， $\text{[math]}$ 中， $\text{[math]}$ ，利用尺规在 $\text{[math]}$ ， $\text{[math]}$ 上分别截取 $\text{[math]}$ ， $\text{[math]}$ ，使 $\text{[math]}$ ；分别以D，E为圆心、以大于 $\text{[math]}$ 为长的半径作弧，两弧在 $\text{[math]}$ 内交于点F；作射线 $\text{[math]}$ 交 $\text{[math]}$ 于点G，若 $\text{[math]}$ ，P为 $\text{[math]}$ 上一动点，则 $\text{[math]}$ 的最小值为（）

A . 无法确定 B . $\text{[math]}$ C . 1 D . 2

答案解析收藏纠错 + 选题
9. (2021·驻马店模拟) 已知二次函数 $\text{[math]}$ ，当x取互为相反数的任意两个实数值时，对应的函数值y总相等，则关于x的一元二次方程 $\text{[math]}$ 的两根之积为（）

A . 0 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2022九下·南召开学考) 在平面直角坐标系 $\text{[math]}$ 中， $\text{[math]}$ 的直角顶点B在y轴上，点A的坐标为 $\text{[math]}$ ，将 $\text{[math]}$ 沿直线 $\text{[math]}$ 翻折，得到 $\text{[math]}$ ，过 $\text{[math]}$ 作 $\text{[math]}$ 垂直于 $\text{[math]}$ 交y轴于点C，则点C的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2024八下·镇赉县月考) 已知： $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
12. (2021·驻马店模拟) 对某条线段的长度进行了3次测量，得到3个结果（单位：mm）9.9，10.1，10.0，若用a作为这条线段长度的近似值，当10.0mm时，最小.对另一条线段的长度进行了n次测量，得到n个结果（单位：mm）x₁ ， x₂ ， …x_n ，若用x作为这条线段长度的近似值，当x＝mm时，（x﹣x₁）²+（x﹣x₂）²+…+（x﹣x_n）²最小.

答案解析收藏纠错 + 选题
13. (2024九下·房山模拟) 在平面直角坐标系 $\text{[math]}$ 中，直线 $\text{[math]}$ 与双曲线 $\text{[math]}$ 交于A，B两点．若点A，B的纵坐标分别为 $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
14. (2021·驻马店模拟) 如图，已知△ABC≌△DCE≌△GEF，三条对应边BC、CE、EF在同一条直线上，连接BG，分别交AC、DC、DE于点P、Q、K，其中S_△_PQC＝3，则图中三个阴影部分的面积和为.

答案解析收藏纠错 + 选题
15. (2022·青岛模拟) 如图，正方形ABCD的边长为a，点E在边AB上运动（不与点A，B重合），∠DAM＝45°，点F在射线AM上，且AF＝ $\text{[math]}$ BE，CF与AD相交于点G，连接EC、EF、EG.则下列结论：①∠ECF＝45°；②△AEG的周长为（1+ $\text{[math]}$ ）a；③BE²+DG²＝EG²；④△EAF的面积的最大值是 $\text{[math]}$ a²；⑤当时BE＝ $\text{[math]}$ a，G是线段AD的中点.其中正确的结论是.

答案解析收藏纠错 + 选题

三、解答题

16. (2024九上·哈尔滨期中) 先化简，再求代数式 $\text{[math]}$ 的值，其中 $\text{[math]}$

答案解析收藏纠错 + 选题
17. (2021·驻马店模拟) 全球新冠肺炎疫情依然严重，境外许多国家的疫情尚在继续蔓延，疫情防控不可松懈.如图是某国截止5月31日新冠病毒感染人数的扇形统计图和折线统计图.

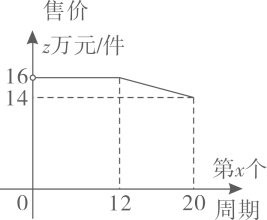
根据上面图表信息，回答下列问题：
1. （1）截止5月31日该国新冠肺炎感染总人数累计为万人，扇形统计图中40﹣59岁感染人数对应圆心角的度数为°；
2. （2）请直接在图中补充完整该国新冠肺炎感染人数的折线统计图；
3. （3）在该国所有新冠肺炎感染病例中随机地抽取1人，求该患者年龄为60岁或60岁以上的概率；
4. （4）若该国感染病例中从低到高各年龄段的死亡率依次为1%，2.75%，3.5%，10%，20%，求该国新冠肺炎感染病例的平均死亡率.
答案解析收藏纠错 + 选题
18. (2021·驻马店模拟) 如图，一艘船由A港沿北偏东65°方向航行34km到B港，然后再沿北偏西42°方向航行至C港，已知C港在A港北偏东20°方向.
1. （1）直接写出∠C的度数；
2. （2）求A、C两港之间的距离.（结果用含非特殊角的三角函数及根式表示即可）
答案解析收藏纠错 + 选题
19. (2022·云南模拟) 某工厂计划在每个生产周期内生产并销售完某型设备，设备的生产成本为10万元/件
1. （1）如图，设第x（0＜x≤20）个生产周期设备售价z万元/件，z与x之间的关系用图中的函数图象表示，求z关于x的函数解析式（写出x的范围）．
2. （2）设第x个生产周期生产并销售的设备为y件，y与x满足关系式y=5x+40（0＜x≤20）．在（1）的条件下，工厂在第几个生产周期创造的利润最大？最大为多少万元？（利润=收入-成本）
答案解析收藏纠错 + 选题
20. (2021·驻马店模拟) 小云在学习过程中遇到一个函数 $\text{[math]}$ ．下面是小云对其探究的过程，请补充完整：
1. （1）当 $\text{[math]}$ 时，对于函数 $\text{[math]}$ ，即 $\text{[math]}$ ，当 $\text{[math]}$ 时， $\text{[math]}$ 随x的增大而，且 $\text{[math]}$ ；对于函数 $\text{[math]}$ ，当 $\text{[math]}$ 时， $\text{[math]}$ 随x的增大而，且 $\text{[math]}$ ；结合上述分析，进一步探究发现，对于函数 $\text{[math]}$ ，当 $\text{[math]}$ 时，y随x的增大而．
2. （2）当 $\text{[math]}$ 时，对于函数 $\text{[math]}$ ，当 $\text{[math]}$ 时，y与x的几组对应值如下表：
  
  x
  
  0
  
  $\text{[math]}$
  
  1
  
  $\text{[math]}$
  
  2
  
  $\text{[math]}$
  
  3
  
  $\text{[math]}$
  
  y
  
  0
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  1
  
  $\text{[math]}$
  
  $\text{[math]}$
  
  $\text{[math]}$
  
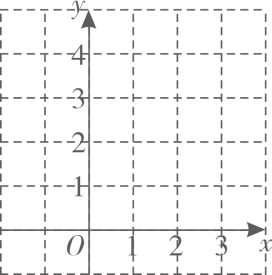
  综合上表，进一步探究发现，当 $\text{[math]}$ 时，y随x的增大而增大．在平面直角坐标系 $\text{[math]}$ 中，画出当 $\text{[math]}$ 时的函数y的图象．
3. （3）过点(0，m)（ $\text{[math]}$ ）作平行于x轴的直线l，结合（1）（2）的分析，解决问题：若直线l与函数 $\text{[math]}$ 的图象有两个交点，则m的最大值是．
答案解析收藏纠错 + 选题
21. (2022·平邑模拟) 古希腊数学家毕达哥拉斯认为：“一切平面图形中最美的是圆”.请研究如下美丽的圆.如图，线段AB是⊙O的直径，延长AB至点C，使BC＝OB，点E是线段OB的中点，DE⊥AB交⊙O于点D，点P是⊙O上一动点（不与点A，B重合），连接CD，PE，PC.
1. （1）求证：CD是⊙O的切线；
2. （2）小明在研究的过程中发现 $\text{[math]}$ 是一个确定的值.回答这个确定的值是多少？并对小明发现的结论加以证明.
答案解析收藏纠错 + 选题
22. (2021·驻马店模拟) 希腊数学家帕普斯给出了一种“三等分锐角”的方法，具体如下：
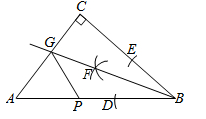
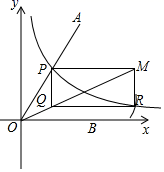
①建立平面直角坐标系，将已知锐角∠AOB的顶点与原点O重合，角的一边OB与x轴正方向重合；

②在平面直角坐标系中，绘制函数 $\text{[math]}$ 的图象，图象与已知角的另一边OA交于点P；

③以P为圆心，2OP为半径作弧，交函数 $\text{[math]}$ 的图象于R点；

④分别过点P和R作x轴和y轴的平行线，两线相交于点M、Q；

⑤连接OM，得到∠MOB，这时∠MOB＝ $\text{[math]}$ ∠AOB.

根据以上材料解答下列问题：
1. （1）设点P的坐标为（a， $\text{[math]}$ ），点R的坐标为（b， $\text{[math]}$ ），则点M的坐标为；
2. （2）求证：点Q在直线OM上；
3. （3）求证：∠MOB＝ $\text{[math]}$ ∠AOB.
答案解析收藏纠错 + 选题
23. (2019九上·交城期末) 请完成下面的几何探究过程：
1. （1）观察填空：如图1，在Rt△ABC中，∠C=90°，AC=BC=4，点D为斜边AB上一动点（不与点A，B重合），把线段CD绕点C顺时针旋转90°得到线段CE，连DE，BE，则
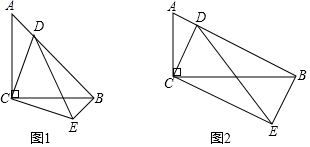
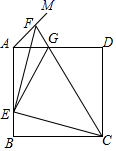
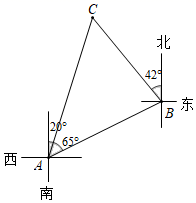
  ①∠CBE的度数为；
  
  ②当BE=时，四边形CDBE为正方形.
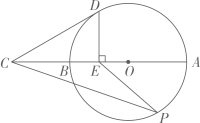
2. （2）探究证明：如图2，在Rt△ABC中，∠C=90°，BC=2AC=4，点D为斜边AB上一动点（不与点A，B重合），把线段CD绕点C顺时针旋转90°后并延长为原来的两倍得到线段CE，连DE，BE则：
  ①在点D的运动过程中，请判断∠CBE与∠A的大小关系，并证明；
  
  ②当CD⊥AB时，求证：四边形CDBE为矩形
3. （3）拓展延伸：如图2，在点D的运动过程中，若△BCD恰好为等腰三角形，请直接写出此时AD的长.
答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

河南省驻马店市、天宏2021年数学中考一模大联考试卷

副标题：

*注意事项：

河南省驻马店市、天宏2021年数学中考一模大联考试卷

试题分析

总体分析

题量分析

难度分析

知识点分析

x	0	$\text{[math]}$	1	$\text{[math]}$	2	$\text{[math]}$	3	$\text{[math]}$
y	0	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	1	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$