北京市师达中学2023年中考四模数学试题

更新时间：2023-08-02 浏览次数：55 类型：中考模拟

一、单选题

1. (2020·北京) 如图是某几何体的三视图，该几何体是（）

A . 圆柱 B . 圆锥 C . 三棱锥 D . 长方体

答案解析收藏纠错 + 选题
2. 2021年2月，中共中央、国务院发布关于全面推进乡村振兴加快农业农村现代化的意见，明确指出加大涉农职业院校、涉农专业建设力度．截止到2021年6月，中国已建成世界上规模最大的职业教育体系，有 $\text{[math]}$ 万所职业学校， $\text{[math]}$ 万在校生．将 $\text{[math]}$ 用科学记数法表示应为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. 将一副三角尺（厚度不计）如图摆放，使 $\text{[math]}$ 边与 $\text{[math]}$ 边互相平行，则图中 $\text{[math]}$ 的大小为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. 实数m，n在数轴上的对应点的位置如图所示，下列结论中正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. 不透明的袋子中装有3个红球、2个白球，除颜色外小球无其他差别．从中随机摸出一个小球，放回并摇匀，再从中随机摸出一个小球，那么两次都摸到红球的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2017·呼兰模拟)
下列图形中，既是轴对称图形又是中心对称图形的有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
7. 已知关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 有两个相等的实数根，则实数 $\text{[math]}$ 的值是（）

A . $\text{[math]}$ B . 0 C . 1 D . 4

答案解析收藏纠错 + 选题
8. 下面的三个问题中都有两个变量：
①矩形的面积一定，一边长 $\text{[math]}$ 与它的邻边 $\text{[math]}$ ；
②某村的耕地面积一定，该村人均耕地面积 $\text{[math]}$ 与全村总人口 $\text{[math]}$ ；
③汽车的行驶速度一定，行驶路程 $\text{[math]}$ 与行驶时间 $\text{[math]}$ ．
其中，两个变量之间的函数关系可以用如图所示的图象表示的是（）

A . ①② B . ①③ C . ②③ D . ①②③

答案解析收藏纠错 + 选题

二、填空题

9. (2021八下·西湖期末) 若 $\text{[math]}$ 在实数范围内有意义，则实数 $\text{[math]}$ 的取值范围是.

答案解析收藏纠错 + 选题
10. (2016·南平模拟) 分解因式：3a²﹣6a+3=．

答案解析收藏纠错 + 选题
11. 方程 $\text{[math]}$ 的解为．

答案解析收藏纠错 + 选题
12. 在平面直角坐标系 $\text{[math]}$ 中，直线 $\text{[math]}$ 与双曲线 $\text{[math]}$ 交于 $\text{[math]}$ ， $\text{[math]}$ 两点．若点 $\text{[math]}$ ， $\text{[math]}$ 的纵坐标分别为 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
13. (2022·北京市) 如图，在矩形 $\text{[math]}$ 中，若 $\text{[math]}$ ，则 $\text{[math]}$ 的长为．

答案解析收藏纠错 + 选题
14. 某班级准备定做一批底色相同的T恤衫，征求了全班40名同学的意向，每个人都选择了一种底色，得到如下数据：
底色
灰色
黑色
白色
紫色
红色
粉色
频数
3
6
18
4
7
2
为了满足大多数人的需求，此次定做的T恤衫的底色为．

答案解析收藏纠错 + 选题
15. 如图， $\text{[math]}$ 是 $\text{[math]}$ 内接正五边形的一条边，点 $\text{[math]}$ 在优弧 $\text{[math]}$ 上，则 $\text{[math]}$ 的度数为 $\text{[math]}$ ．

答案解析收藏纠错 + 选题

16. 某工厂用甲、乙两种原料制作 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三种型号的工艺品，三种型号工艺品的重量及所含甲、乙两种原料的重量如下：

工艺品型号	含甲种原料的重量 $\text{[math]}$	含乙种原料的重量 $\text{[math]}$	工艺品的重量 $\text{[math]}$
A	3	4	7
B	3	2	5
C	2	3	5

现要用甲、乙两种原料共 $\text{[math]}$ ，制作5个工艺品，且每种型号至少制作1个．

（1）若 $\text{[math]}$ 原料恰好全部用完，则制作 $\text{[math]}$ 型工艺品的个数为个；
（2）若使用甲种原料不超过 $\text{[math]}$ ，同时使用乙种原料最多，则制作方案中 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 三种型号的工艺品的个数依次为．

答案解析收藏纠错 + 选题

三、解答题

17. 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. 解不等式组： $\text{[math]}$

答案解析收藏纠错 + 选题
19. 已知 $\text{[math]}$ ，求代数式 $\text{[math]}$ 的值．

答案解析收藏纠错 + 选题

20. 下面是小芸同学证明定理时使用的两种添加辅助线的方法，选择其中一种，完成证明．

定理：直角三角形斜边上的中线等于斜边的一半．已知：如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 边的中点．

求证： $\text{[math]}$ ．

方法一：

证明：延长 $\text{[math]}$ 至 $\text{[math]}$ ，使 $\text{[math]}$ ，

连接 $\text{[math]}$ ， $\text{[math]}$ ．

方法二：

证明：过点 $\text{[math]}$ 作 $\text{[math]}$ 于点 $\text{[math]}$ ．

答案解析收藏纠错 + 选题

21. 如图，四边形 $\text{[math]}$ 是平行四边形，点 $\text{[math]}$ ， $\text{[math]}$ 分别是 $\text{[math]}$ ， $\text{[math]}$ 上的点，且 $\text{[math]}$ ．
1. （1）求证：四边形 $\text{[math]}$ 是平行四边形；
2. （2）连接 $\text{[math]}$ ，若 $\text{[math]}$ 平分 $\text{[math]}$ ，求证：四边形 $\text{[math]}$ 是菱形．
答案解析收藏纠错 + 选题
22. 在平面直角坐标系 $\text{[math]}$ 中，一次函数 $\text{[math]}$ （ $\text{[math]}$ ）的图象由函数 $\text{[math]}$ 的图象平移得到，且经过点 $\text{[math]}$ ．
1. （1）求这个一次函数的解析式；
2. （2）当 $\text{[math]}$ 时，对于 $\text{[math]}$ 的每一个值，函数 $\text{[math]}$ （ $\text{[math]}$ ）的值小于一次函数 $\text{[math]}$ 的值，直接写出 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
23. 如图， $\text{[math]}$ 是 $\text{[math]}$ 的外接圆， $\text{[math]}$ 是 $\text{[math]}$ 的直径，分别过 $\text{[math]}$ ， $\text{[math]}$ 两点作 $\text{[math]}$ 的切线，交点为点 $\text{[math]}$ ，连接 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ．
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
24. $\text{[math]}$ 年 $\text{[math]}$ 月 $\text{[math]}$ 日，“天宫课堂”第三课在中国空间站的问天实验舱开讲，“太空教师”陈冬、刘洋、蔡旭哲为广大青少年带来一场精彩的太空科普课．为了激发学生的航天兴趣，弘扬科学精神，某校甲、乙两个校区的八年级所有学生（两个校区八年级各有 $\text{[math]}$ 名学生）参加了“格物致知叩问苍穹”为主题的太空科普知识竞赛．为了解八年级学生的太空科普知识掌握情况，从每个校区八年级的科技小组中分别随机抽取了 $\text{[math]}$ 名学生的竞赛成绩，并整理成部分信息如下：
a．乙校区学生成绩的频数分布直方图如下（数据分为5组： $\text{[math]}$ ； $\text{[math]}$ ； $\text{[math]}$ ； $\text{[math]}$ ； $\text{[math]}$ ）：

b．乙校区的学生成绩数据在 $\text{[math]}$ 这一组的是：
91
91
92
94
c．两个校区学生成绩的平均数、中位数、方差如下表所示：
校区
平均数
中位数
方差
甲校区
89.3
88.5
42.6
乙校区
89.3
m
87.2
根据上述信息，解答问题：
1. （1） $\text{[math]}$ ；
2. （2）对于抽取的八年级学生竞赛成绩，高于本校区平均分的人数更多的是校区，成绩更整齐的是校区（填“甲”或“乙”）；
3. （3）抽样调查中，两个校区共有30%的学生竞赛成绩不低于95分．该校计划从两个校区选派成绩不低于95分的学生参加全区的竞赛，估计参赛的八年级学生中，甲校区有人被选中．
答案解析收藏纠错 + 选题
25. 某公园修建一个圆形喷水池，在池中心竖直安装一根水管，在水管的顶端安装一个可调节角度的喷水头，从喷水头喷出的水柱形状是一条抛物线．建立如图所示的平面直角坐标系，抛物线形水柱的竖直高度 $\text{[math]}$ （单位：m）与到池中心的水平距离 $\text{[math]}$ （单位：m）满足的关系式近似为 $\text{[math]}$ （ $\text{[math]}$ ）．
1. （1）在某次安装调试过程中，测得 $\text{[math]}$ 与 $\text{[math]}$ 的部分对应值如下表：
  水平距离 $\text{[math]}$
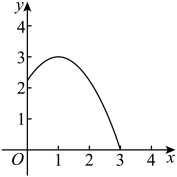
  0
  0.5
  1
  1.5
  2
  2.5
  3
  竖直高度 $\text{[math]}$
  2.25
  2.8125
  3
  2.8125
  2.25
  1.3125
  0
  根据表格中的数据，解答下列问题：
  ①水管的长度是m；
  ②求出 $\text{[math]}$ 与 $\text{[math]}$ 满足的函数解析式 $\text{[math]}$ （ $\text{[math]}$ ）；
2. （2）安装工人在上述基础上进行了下面两种调试：
  ①不改变喷水头的角度，将水管长度增加1m，水柱落地时与池中心的距离为 $\text{[math]}$ ；
  ②不改变水管的长度，调节喷水头的角度，使得水柱满足 $\text{[math]}$ ，水柱落地时与池中心的距离为 $\text{[math]}$ ．则比较 $\text{[math]}$ 与 $\text{[math]}$ 的大小关系是： $\text{[math]}$ $\text{[math]}$ （填“ $\text{[math]}$ ”或“ $\text{[math]}$ ”或“ $\text{[math]}$ ”）
答案解析收藏纠错 + 选题
26. 在平面直角坐标系 $\text{[math]}$ 中，点 $\text{[math]}$ ， $\text{[math]}$ 在抛物线 $\text{[math]}$ 上，且 $\text{[math]}$ ．
1. （1）当 $\text{[math]}$ ， $\text{[math]}$ 时，求 $\text{[math]}$ 的值；
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
27. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，点 $\text{[math]}$ 是 $\text{[math]}$ 边上一个动点（不与 $\text{[math]}$ ， $\text{[math]}$ 重合），连接 $\text{[math]}$ ，将线段 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转 $\text{[math]}$ ，得到线段 $\text{[math]}$ ，连接 $\text{[math]}$ ．
1. （1）求 $\text{[math]}$ 的度数；
2. （2）过点 $\text{[math]}$ 作 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ，交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，交 $\text{[math]}$ 于点 $\text{[math]}$ ；
  ①依据题意，补全图形；
  ②用等式表示线段 $\text{[math]}$ ， $\text{[math]}$ 的数量关系，并证明．
答案解析收藏纠错 + 选题
28. 在平面直角坐标系 $\text{[math]}$ 中， $\text{[math]}$ 的半径为1， $\text{[math]}$ 为 $\text{[math]}$ 上一点，点 $\text{[math]}$ ．
对于点 $\text{[math]}$ 给出如下定义：将点 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转90°，得到点 $\text{[math]}$ ，点 $\text{[math]}$ 关于点 $\text{[math]}$ 的对称点为 $\text{[math]}$ ，称点 $\text{[math]}$ 为点 $\text{[math]}$ 关于点 $\text{[math]}$ ， $\text{[math]}$ 的“中旋点”．
1. （1）如图1，已知点 $\text{[math]}$ ，点 $\text{[math]}$ 为点 $\text{[math]}$ 关于点 $\text{[math]}$ ， $\text{[math]}$ 的“中旋点”．
  ①若点 $\text{[math]}$ ，在图中画出点 $\text{[math]}$ ，并直接写出 $\text{[math]}$ 的长度为；
  
  ②当点 $\text{[math]}$ 在 $\text{[math]}$ 上运动时，直线 $\text{[math]}$ 上存在点 $\text{[math]}$ 关于点 $\text{[math]}$ ， $\text{[math]}$ 的“中旋点” $\text{[math]}$ ，求 $\text{[math]}$ 的取值范围；
2. （2）点 $\text{[math]}$ ，当点 $\text{[math]}$ 在 $\text{[math]}$ 上运动时，若 $\text{[math]}$ 上存在点 $\text{[math]}$ 关于点 $\text{[math]}$ ， $\text{[math]}$ 的“中旋点” $\text{[math]}$ ，直接写出 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题