河南省2020年中考数学试卷

更新时间：2020-07-31 浏览次数：997 类型：中考真卷

一、选择题

1. (2021九上·玉屏期末) 2的相反数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 2 D . -2

答案解析收藏纠错 + 选题
2. (2023九上·郑州经济技术开发月考) 如下摆放的几何体中，主视图与左视图有可能不同的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
3. (2022七下·武昌期末) 要调查下列问题，适合采用全面调查(普查)的是（）

A . 中央电视台《开学第--课》的收视率 B . 某城市居民6月份人均网上购物的次数 C . 即将发射的气象卫星的零部件质量 D . 某品牌新能源汽车的最大续航里程

答案解析收藏纠错 + 选题
4. (2021七下·三门峡期中) 如图， $\text{[math]}$ ，若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. 电子文件的大小常用 $\text{[math]}$ 等作为单位，其中 $\text{[math]}$ ，某视频文件的大小约为 $\text{[math]}$ 等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2020·河南) 若点 $\text{[math]}$ 在反比例函数 $\text{[math]}$ 的图像上，则 $\text{[math]}$ 的大小关系为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2024九下·涟水模拟) 定义运算： $\text{[math]}$ .例如 $\text{[math]}$ .则方程 $\text{[math]}$ 的根的情况为（）

A . 有两个不相等的实数根 B . 有两个相等的实数根 C . 无实数根 D . 只有一个实数根

答案解析收藏纠错 + 选题
8. (2024八下·张店期末) 国家统计局统计数据显示，我国快递业务收入逐年增加.2017年至2019年我国快递业务收入由5000亿元增加到7500亿元.设我国2017年至2019年快递业务收入的年平均增长率为x.则可列方程为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2022·淮南模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ .边 $\text{[math]}$ 在x轴上，顶点 $\text{[math]}$ 的坐标分别为 $\text{[math]}$ 和 $\text{[math]}$ .将正方形 $\text{[math]}$ 沿x轴向右平移当点E落在 $\text{[math]}$ 边上时，点D的坐标为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2022·曹县模拟) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，分别以点 $\text{[math]}$ 为圆心， $\text{[math]}$ 的长为半径作弧，两弧交于点D，连接 $\text{[math]}$ 则四边形 $\text{[math]}$ 的面积为（）

A . $\text{[math]}$ B . 9 C . 6 D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2024七下·福州期中) 请写出一个大于1且小于2的无理数：.

答案解析收藏纠错 + 选题
12. (2022七下·广陵期末) 已知关于 $\text{[math]}$ 的不等式组 $\text{[math]}$ ，其中 $\text{[math]}$ 在数轴上的对应点如图所示，则这个不等式组的解集为.

答案解析收藏纠错 + 选题
13. (2020·河南) 如图所示的转盘，被分成面积相等的四个扇形，分别涂有红、黄、蓝、绿四种颜色.固定指针，自由转动转盘两次，每次停止后，记下指针所指区域(指针指向区域分界线时，忽略不计)的颜色，则两次颜色相同的概率是.

答案解析收藏纠错 + 选题
14. (2022九上·郑州开学考) 如图，在边长为 $\text{[math]}$ 的正方形 $\text{[math]}$ 中，点 $\text{[math]}$ 分别是边 $\text{[math]}$ 的中点，连接 $\text{[math]}$ 点 $\text{[math]}$ 分别是 $\text{[math]}$ 的中点，连接 $\text{[math]}$ ，则 $\text{[math]}$ 的长度为.

答案解析收藏纠错 + 选题
15. (2020·河南) 如图，在扇形 $\text{[math]}$ 中， $\text{[math]}$ 平分 $\text{[math]}$ 交狐 $\text{[math]}$ 于点D.点E为半径 $\text{[math]}$ 上一动点若 $\text{[math]}$ ，则阴影部分周长的最小值为.

答案解析收藏纠错 + 选题

三、解答题

16. (2023九下·襄阳模拟) 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$

答案解析收藏纠错 + 选题
17. (2020·河南) 为发展乡村经济，某村根据本地特色，创办了山药粉加工厂.该厂需购置一台分装机，计划从商家推荐试用的甲、乙两台不同品牌的分装机中选择.试用时，设定分装的标准质量为每袋 $\text{[math]}$ ，与之相差大于 $\text{[math]}$ 为不合格.为检验分装效果，工厂对这两台机器分装的成品进行了抽样和分析，过程如下：
[收集数据]从甲、乙两台机器分装的成品中各随机抽取 $\text{[math]}$ 袋，测得实际质量(单位： $\text{[math]}$ )

如下：

甲： $\text{[math]}$ $\text{[math]}$

乙： $\text{[math]}$ $\text{[math]}$

[整理数据]整理以上数据，得到每袋质量 $\text{[math]}$ 的频数分布表.

485≤x<490 490≤x<495 495≤x<500 500≤x<505 505≤x<510 510≤x<515

甲 2 2 4 7 4 1

乙 1 3 5 7 3 1

[分析数据]根据以上数据，得到以下统计量.

平均数中位数方差不合格率

甲 499.7 501.5 42.01 b

乙 499.7 a 31.81 10%

根据以上信息，回答下列问题：
1. （1）表格中的 $\text{[math]}$ $\text{[math]}$
2. （2）综合上表中的统计量，判断工厂应选购哪一台分装机，并说明理由.
答案解析收藏纠错 + 选题
18. (2022·薛城模拟) 位于河南省登封市境内的元代观星台，是中国现存最早的天文台，也是世界文化遗产之一.

某校数学社团的同学们使用卷尺和自制的测角仪测量观星台的高度.如图所示，他们在地面一条水平步道 $\text{[math]}$ 上架设测角仪，先在点M处测得观星台最高点A的仰角为 $\text{[math]}$ ，然后沿 $\text{[math]}$ 方向前进 $\text{[math]}$ 到达点N处，测得点 $\text{[math]}$ 的仰角为 $\text{[math]}$ .测角仪的高度为 $\text{[math]}$ ，
1. （1）求观星台最高点A距离地面的高度(结果精确到 $\text{[math]}$ .参考数据： $\text{[math]}$ )；
2. （2） “景点简介”显示，观星台的高度为 $\text{[math]}$ ，请计算本次测量结果的误差，并提出一条减小误差的合理化建议.
答案解析收藏纠错 + 选题
19. (2022七上·桓台期末) 暑期将至，某健身俱乐部面向学生推出暑期优惠活动，活动方案如下.
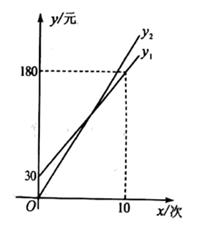
方案一：购买一张学生暑期专享卡，每次健身费用按六折优惠；

方案二：不购买学生暑期专享卡，每次健身费用按八折优惠；

设某学生暑期健身x(次)，按照方案一所需费用为 $\text{[math]}$ ，(元)，且 $\text{[math]}$ ；按照方案二所需费用为 $\text{[math]}$ (元) ，且 $\text{[math]}$ 其函数图象如图所示.
1. （1）求 $\text{[math]}$ 和b的值，并说明它们的实际意义；
2. （2）求打折前的每次健身费用和 $\text{[math]}$ 的值；
3. （3）八年级学生小华计划暑期前往该俱乐部健身8次，应选择哪种方案所需费用更少?说明理由.
答案解析收藏纠错 + 选题
20. (2020·河南) 我们学习过利用用尺规作图平分一个任意角，而“利用尺规作图三等分一个任意角”曾是数学史上一大难题，之后被数学家证明是不可能完成的人们根据实际需爱，发明了一种简易操作工具--------三分角器.图1是它的示意图，其中 $\text{[math]}$ 与半圆O的直径 $\text{[math]}$ 在同一直线上，且 $\text{[math]}$ 的长度与半圆的半径相等； $\text{[math]}$ 与 $\text{[math]}$ 重直F点 $\text{[math]}$ 足够长.
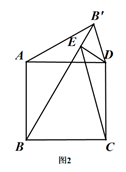
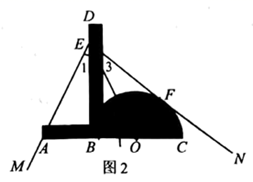
使用方法如图2所示，若要把 $\text{[math]}$ 三等分，只需适当放置三分角器，使 $\text{[math]}$ 经过 $\text{[math]}$ 的顶点 $\text{[math]}$ ，点 $\text{[math]}$ 落在边 $\text{[math]}$ 上，半圆O与另一边 $\text{[math]}$ 恰好相切，切点为F，则 $\text{[math]}$ 就把 $\text{[math]}$ 三等分了.

为了说明这一方法的正确性，需要对其进行证明.如下给出了不完整的“已知”和“求证”，请补充完整，并写出“证明”过程.

已知：如图2，点在 $\text{[math]}$ 同一直线上， $\text{[math]}$ 垂足为点B， ▲

求证： ▲

答案解析收藏纠错 + 选题
21. 如图，抛物线 $\text{[math]}$ 与x轴正半轴，y轴正半轴分别交于点 $\text{[math]}$ ，且 $\text{[math]}$ 点G为抛物线的顶点.
1. （1）求抛物线的解析式及点G的坐标；
2. （2）点 $\text{[math]}$ 为抛物线上两点(点M在点N的左侧) ，且到对称轴的距离分别为3个单位长度和5个单位长度，点Q为抛物线上点 $\text{[math]}$ 之间(含点 $\text{[math]}$ )的一个动点，求点Q的纵坐标 $\text{[math]}$ 的取值范围.
答案解析收藏纠错 + 选题
22. (2020·河南) 小亮在学习中遇到这样一个问题：
如图，点D是弧 $\text{[math]}$ 上一动点，线段 $\text{[math]}$ 点A是线段 $\text{[math]}$ 的中点，过点C作 $\text{[math]}$ ，交 $\text{[math]}$ 的延长线于点F.当 $\text{[math]}$ 为等腰三角形时，求线段 $\text{[math]}$ 的长度.

小亮分析发现，此问题很难通过常规的推理计算彻底解决，于是尝试结合学习函数的经验研究此问题，请将下面的探究过程补充完整：
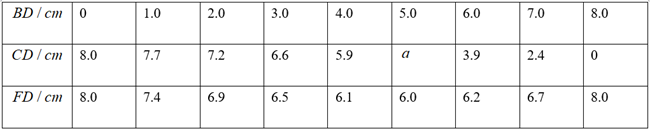
1. （1）根据点D在弧 $\text{[math]}$ 上的不同位置，画出相应的图形，测量线段 $\text{[math]}$ 的长度，得到下表的几组对应值.
  
  操作中发现：
  
  ①"当点D为弧 $\text{[math]}$ 的中点时， $\text{[math]}$ ".则上中a的值是
  
  ②"线段 $\text{[math]}$ 的长度无需测量即可得到".请简要说明理由；
2. （2）将线段 $\text{[math]}$ 的长度作为自变量 $\text{[math]}$ 和 $\text{[math]}$ 的长度都是x的函数，分别记为 $\text{[math]}$ 和 $\text{[math]}$ ，并在平面直角坐标系 $\text{[math]}$ 中画出了函数 $\text{[math]}$ 的图象，如图所示.请在同一坐标系中画出函数 $\text{[math]}$ 的图象；
3. （3）继续在同一坐标系中画出所需的函数图象，并结合图象直接写出：当 $\text{[math]}$ 为等腰三角形时，线段 $\text{[math]}$ 长度的近似值.(结果保留一位小数).
答案解析收藏纠错 + 选题
23. (2021·潜江模拟) 将正方形 $\text{[math]}$ 的边 $\text{[math]}$ 绕点A逆时针旋转至 $\text{[math]}$ ，记旋转角为 $\text{[math]}$ .连接 $\text{[math]}$ ，过点D作 $\text{[math]}$ 垂直于直线 $\text{[math]}$ ，垂足为点E，连接 $\text{[math]}$ ，
1. （1）如图1，当 $\text{[math]}$ 时， $\text{[math]}$ 的形状为，连接 $\text{[math]}$ ，可求出 $\text{[math]}$ 的值为；
2. （2）当 $\text{[math]}$ 且 $\text{[math]}$ 时，
  ①（1）中的两个结论是否仍然成立?如果成立，请仅就图2的情形进行证明；如果不成立，请说明理由；
  
  ②当以点 $\text{[math]}$ 为顶点的四边形是平行四边形时，请直接写出 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题