 B .
B .  C .
C .  D .
D . 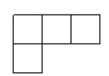
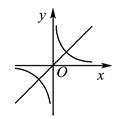 B .
B . 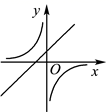 C .
C . 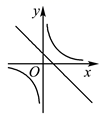 D .
D . 

在学习了直角三角形的边角关系后,小颖和小明两个学习小组继续探究任意锐角三角形的边角关系:在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c.
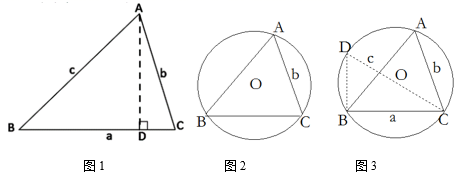
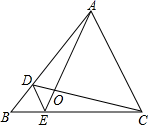
如图1,过A作AD⊥BC于D,则sinB= ,sinC=
即AD=csinB,AD=bsinC,于是=即
,同理有
,
则有
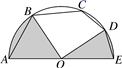
如图2,△ABC的外接圆半径为R,连结CO并延长交⊙O于点D,连结DB,则∠D=∠A,
∵CD为⊙O的直径,∴∠DBC=90°,
在Rt△DBC中,
∵ ,
∴ ,
同理: ,
则有
请你将这一结论用文字语言描述出来:.
小颖学习小组在证明过程中略去了“ ”的证明过程,请你把“
”的证明过程补写出来.
规划局为了方便居民,计划在三个住宅小区A、B、C之间修建一座学校,使它到三个住宅小区的距离相等,已知小区C在小区B的正东方向 千米处,小区A在小区B的东北方向,且A与C之间相距
千米,求学校到三个小区的距离及小区A在小区C的什么方向?