 B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
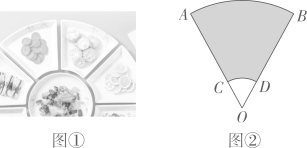

| 甲 | | | | | | |
| 乙 | | | | | | |
由于甲,乙两名运动员的成绩的平均数相同,学校决定依据他们成绩的稳定性进行选拔,那么被选中的运动员是.

请根据图中信息,解答下列问题:
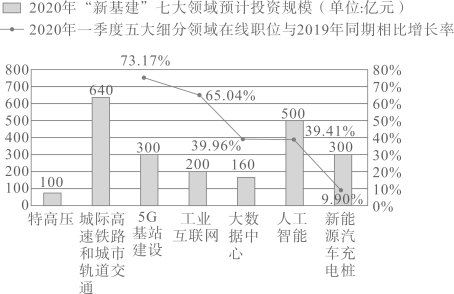
下面是小宇同学的数学日记,请仔细阅读并完成相应的任务.
×年×月×日 星期日
没有直角尺也能作出直角
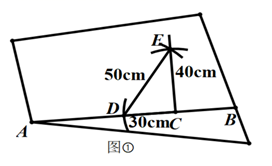
今天,我在书店一本书上看到下面材料:木工师傅有一块如图①所示的四边形木板,他已经在木板上画出一条裁割线 ,现根据木板的情况,要过
上的一点
,作出
的垂线,用锯子进行裁割,然而手头没有直角尺,怎么办呢?
办法一:如图①,可利用一把有刻度的直尺在 上量出
,然后分别以
,
为圆心,以
与
为半径画圆弧,两弧相交于点
,作直线
,则
必为
.

办法二:如图②,可以取一根笔直的木棒,用铅笔在木棒上点出 ,
两点,然后把木棒斜放在木板上,使点
与点
重合,用铅笔在木板上将点
对应的位置标记为点
,保持点
不动,将木棒绕点
旋转,使点
落在
上,在木板上将点
对应的位置标记为点
.然后将
延长,在延长线上截取线段
,得到点
,作直线
,则
.
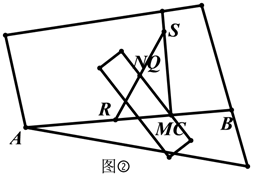
我有如下思考:以上两种办法依据的是什么数学原理呢?我还有什么办法不用直角尺也能作出垂线呢?
……
任务:
②说明你的作法依据的数学定理或基本事实(写出一个即可)

解决问题: