 B .
B .  C .
C .  D .
D . 
|
5640 |
6430 |
6520 |
6798 |
7325 |
|
8430 |
8215 |
7453 |
7446 |
6754 |
|
7638 |
6834 |
7326 |
6830 |
8648 |
|
8752 |
9450 |
9865 |
7290 |
7850 |
对这20个数据按组距1000进行分组,并统计整理,绘制了如下不完整的统计图表.
|
组别 |
步数分组 |
|
A |
|
|
B |
|
|
C |
|
|
D |
|
|
E |
|

根据以上信息解答下列问题:

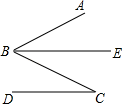
如图, 是
的弦,点
是
上的一点,在直线
上方找一点
,使得
,画出
,并说明理由;
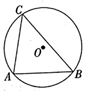
如图, 是
的弦,直线
与
相切于点
,点
,是直线
上异于点
的任意一点,请在图中画出图形,试判断
的大小关系;并说明理由;
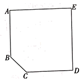
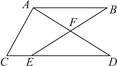
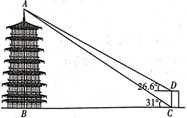
如图,有一个平面图为五边形ABCDE的展览馆,其中 ,
,
.展览馆保卫人员想在线段
上选一点
安装监控装置,用来监视边
,现只要使
最大,就可以让监控装置的效果达到最佳,问在线段
上是否存在点
,使
最大?若存在,请求出符合条件的
的长,若不存在,请说明理由.