湖北省武汉市武昌区部分学校2021届九年级上学期数学10月月...

更新时间：2020-12-11 浏览次数：227 类型：月考试卷

一、单选题

1. (2020九上·武昌月考) 若关于x的方程（a+1）x²+2x﹣1＝0是一元二次方程，则a的取值范围是（）

A . a≠﹣1 B . a＞﹣1 C . a＜﹣1 D . a≠0

答案解析收藏纠错 + 选题
2. (2020九上·武昌月考) 方程 $\text{[math]}$ 的二次项系数、一次项系数、常数项分别为（）

A . 6，2，9 B . 2，－6，9 C . 2，－6，－9 D . 2，6，－9

答案解析收藏纠错 + 选题
3. (2020九上·武昌月考) 下列关于x的一元二次方程中，有两个不相等的实数根的方程是（）

A . x²+4=0 B . 4x²-4x+1=0 C . x²+x+3=0 D . x²+2x-1=0

答案解析收藏纠错 + 选题
4. (2023九上·惠阳月考) 抛物线 $\text{[math]}$ 可由抛物线 $\text{[math]}$ 如何平移得到的（）

A . 先向左平移3个单位，再向下平移2个单位 B . 先向左平移6个单位，再向上平移7个单位 C . 先向上平移2个单位，再向左平移3个单位 D . 先回右平移3个单位，再向上平移2个单位

答案解析收藏纠错 + 选题
5. (2021八下·贵池期末) 三角形两边的长是3和4，第三边的长是方程x²-12x+35=0的根，则该三角形的周长为（）

A . 14 B . 12 C . 12或14 D . 以上都不对

答案解析收藏纠错 + 选题
6. (2023九上·从江月考)
公园有一块正方形的空地，后来从这块空地上划出部分区域栽种鲜花（如图），原空地一边减少了1m，另一边减少了2m，剩余空地的面积为18m² ，求原正方形空地的边长．设原正方形的空地的边长为xm，则可列方程为（　　）

A . （x+1）（x+2）=18 B . x²﹣3x+16=0 C . （x﹣1）（x﹣2）=18 D . x²+3x+16=0

答案解析收藏纠错 + 选题
7. (2021九上·余杭期末) 关于二次函数y=2x²+x-1，下列说法正确的是（）

A . 图象与y轴的交点坐标为(0，1) B . 图象的对称轴在y轴的右侧 C . 当x＜0时，y的值随x值的增大而减小 D . y的最小值为- $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2024九上·官渡开学考) 已知二次函数y＝ax $\text{[math]}$ －2ax＋1（a＜0）图象上三点A(－1，y₁)、B(2，y₂)、C(4，y₃)，则y₁ ， y₂ ， y₃的大小关系为（）

A . y₁＜y₂＜y₃ B . y₂＜y₁＜y₃ C . y₁＜y₃＜y₂ D . y₃＜y₁＜y₂

答案解析收藏纠错 + 选题
9. (2020九上·武昌月考) 有两个一元二次方程M：ax²＋bx＋c＝0；N：cx²＋bx＋a＝0，其中a·c≠0，a≠c，下列四个结论中，错误的是（）

A . 如果方程M有两个相等的实数根，那么方程N也有两个相等的实数根 B . 如果方程M的两根符号相同，那么方程N的两根符号也相同 C . 如果5是方程M的一个根，那么 $\text{[math]}$ 是方程N的一个根 D . 如果方程M和方程N有一个相同的根，那么这个根必是x＝1

答案解析收藏纠错 + 选题
10. (2020九上·武昌月考) 已知关于x的方程|x²+ax|=4有四个不相等的实数根，则a的取值范围是（）

A . $\text{[math]}$ 或 $\text{[math]}$ B . $\text{[math]}$ 或 $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2020九上·武昌月考) 抛物线y＝2x²﹣4x+8的对称轴是.

答案解析收藏纠错 + 选题
12. (2021九上·丰县期中) 把二次三项式 $\text{[math]}$ 化成 $\text{[math]}$ 的形式应为.

答案解析收藏纠错 + 选题
13. (2020九上·武汉月考) 已知抛物线 $\text{[math]}$ ，当x时，y随x的增大而增大.

答案解析收藏纠错 + 选题
14. (2020九上·武昌月考) 飞机着陆后滑行的距离y(单位：m)关于滑行时间t(单位：s)的函数解析式是 $\text{[math]}$ ，飞机着陆后滑行m才能停下来.

答案解析收藏纠错 + 选题
15. (2020九上·武昌月考) 二次函数y＝ax²＋bx＋c（a≠0）的图象如图，给出下列四个结论：①abc＜0 ；② 4a＋c＜2b ；③m(am＋b)+b>a（m≠－1）；④方程ax²＋bx＋c-3＝0的两根为x₁ ， x₂（x₁<x₂)，则x₂<1，x₁>－3 ，其中正确结论的是.

答案解析收藏纠错 + 选题
16. (2020九上·武昌月考) 已知抛物线 y= -x²+ mx +2m ，当-1 ≤ x ≤ 2时，对应的函数值y的最大值是6，则 m的值是.

答案解析收藏纠错 + 选题

三、解答题

17. (2023八下·合肥期末) 解方程： $\text{[math]}$

答案解析收藏纠错 + 选题
18. (2021九上·博兴期中) 某地区2013年投入教育经费2500万元，2015年投入教育经费3025万元．
1. （1）求2013年至2015年该地区投入教育经费的年平均增长率
2. （2）根据（1）所得的年平均增长率，预计2016年该地区将投入教育经费多少万元
答案解析收藏纠错 + 选题
19. (2020九上·武昌月考) 若关于x的一元二次方程x²－3x＋p=0有两个不相等的实数根分别为a和b、且a²-ab+b²=18.
1. （1）求p的值；
2. （2）求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
20. (2020九上·武昌月考) 如图，抛物线y＝ax²+bx过点P（﹣1，5），A（4，0）.
1. （1）求抛物线的解析式；
2. （2）在第一象限内的抛物线上有一点B，当PA⊥PB时，求点B的坐标.
答案解析收藏纠错 + 选题
21. (2024八上·益阳开学考) ▱ABCD中，点E在AD上，DE=CD，请仅用无刻度的直尺，按要求作图（保留作图痕迹，不写作法）
1. （1）在图1中，画出∠C的角平分线；
2. （2）在图2中，画出∠A的角平分线.
答案解析收藏纠错 + 选题
22. (2021九上·广饶期中) “武汉加油!中国加油!”疫情牵动万人心，每个人都在为抗击疫情而努力.某厂改造了 $\text{[math]}$ 条口罩生产线，每条生产线每天可生产口罩 $\text{[math]}$ 个.如果每增加一条生产线，每条生产线就会比原来少生产 $\text{[math]}$ 个口罩.设增加 $\text{[math]}$ 条生产线后，每条生产线每天可生产口罩 $\text{[math]}$ 个.
1. （1）直接写出 $\text{[math]}$ 与 $\text{[math]}$ 之间的函数关系式；
2. （2）若每天共生产口罩 $\text{[math]}$ 个，在投入人力物力尽可能少的情况下，应该增加几条生产线?
3. （3）设该厂每天可以生产的口罩 $\text{[math]}$ 个，请求出 $\text{[math]}$ 与 $\text{[math]}$ 的函数关系式，并求出增加多少条生产线时，每天生产的口罩数量最多，最多为多少个?
答案解析收藏纠错 + 选题
23. (2020九上·武昌月考)
1. （1）问题背景.
  如图1，在四边形ABCD中，AB=AD，∠B+∠D=180°，E、F分别是线段BC、线段CD上的点.若∠BAD=2∠EAF，试探究线段BE、EF、FD之间的数量关系.
  
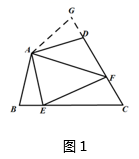
  童威同学探究此问题的方法是，延长FD到点G.使DG=BE.连接AG，先证明△ABE≌△ADG.再证明△AEF≌△AGF，可得出结论，他的结论应是.
2. （2）猜想论证.
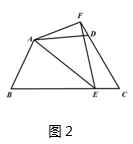
  如图2，在四边形ABCD中，AB=AD，∠B+∠ADC=180°，E在线段BC上、F在线段CD延长线上. 若∠BAD=2∠EAF，上述结论是否依然成立？若成立说明理由；若不成立，试写出相应的结论并给出你的证明.
3. （3）拓展应用.
  如图3，在四边形ABCD中，∠BDC=45°，连接BC、AD，AB：AC：BC=3：4：5，AD=4，且∠ABD+∠CBD=180°.则△ACD的面积为
答案解析收藏纠错 + 选题
24. (2020九上·武昌月考) 抛物线G： $\text{[math]}$ 与 $\text{[math]}$ 轴交于A、B两点，与 $\text{[math]}$ 交于C（0，-1），且AB =4OC.
1. （1）直接写出抛物线G的解析式：；
2. （2）如图1，点D（-1，m）在抛物线G上，点P是抛物线G上一个动点，且在直线OD的下方，过点P作 $\text{[math]}$ 轴的平行线交直线OD于点Q，当线段PQ取最大值时，求点P的坐标；
3. （3）如图2，点M在 $\text{[math]}$ 轴左侧的抛物线G上，将点M先向右平移4个单位后再向下平移，使得到的对应点N也落在 $\text{[math]}$ 轴左侧的抛物线G上，若S_△CMN=2，求点M的坐标.
答案解析收藏纠错 + 选题