四川省成都市西川中学2020-2021学年九年级上学期数学第...

更新时间：2024-07-31 浏览次数：251 类型：月考试卷

一、单选题

1. (2020九上·成都月考) 下列函数关系式中，一定是二次函数的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2020九上·成都月考) 锐角三角函数tan30°的值是（）

A . 1 B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021九上·大邑期中) 在同一直角坐标系中反比例函数 $\text{[math]}$ 与一次函数 $\text{[math]}$ 的图象大致是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2020九上·成都月考) 将抛物线 $\text{[math]}$ 向右平移2个单位长度，再向下平移3个单位，所得到的新抛物线的顶点坐标是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2020九上·成都月考) 若二次函数 $\text{[math]}$ 的图象与 $\text{[math]}$ 轴有两个交点，则关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 的根的情况是（）

A . 有两个不相等的实数根 B . 有两个相等的实数根 C . 没有实数根 D . 不能确定

答案解析收藏纠错 + 选题
6. (2020九上·成都月考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，四边形 $\text{[math]}$ 的面积为21，则 $\text{[math]}$ 的面积是（）

A . $\text{[math]}$ B . 25 C . 35 D . 63

答案解析收藏纠错 + 选题
7. (2023八下·洛宁期中) 如图，点B在反比例函数 $\text{[math]}$ （ $\text{[math]}$ ）的图象上，点C在反比例函数 $\text{[math]}$ （ $\text{[math]}$ ）的图象上，且 $\text{[math]}$ 轴， $\text{[math]}$ ，垂足为点C ，交y轴于点A ，则 $\text{[math]}$ 的面积为（）

A . 3 B . 4 C . 5 D . 6

答案解析收藏纠错 + 选题
8. (2023九上·开福开学考) 某厂一月份生产某大型机器2台，计划二、三月份共生产9台，设二、三月份每月生产台数的月平均增长率为 $\text{[math]}$ ，根据题意列出的方程是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2020九上·成都月考) 如图，小红在作线段AB的垂直平分线时，是这样操作的：分别以点A，B为圆心，大于线段AB长度一半的长为半径画弧，相交于点C，D，则直线CD即为所求。连结AC，BC，AD，BD，根据她的作图方法可知，四边形ADBC定是（）

A . 矩形 B . 正方形 C . 菱形 D . 平行四边形

答案解析收藏纠错 + 选题
10. (2020九上·成都月考) 如图是抛物线 $\text{[math]}$ 图象的一部分，抛物线的顶点坐标是 $\text{[math]}$ ，与 $\text{[math]}$ 轴的一个交点 $\text{[math]}$ ，直线 $\text{[math]}$ 与抛物线交于 $\text{[math]}$ ， $\text{[math]}$ 两点，下列结论：① $\text{[math]}$ ；② $\text{[math]}$ ；③方程 $\text{[math]}$ 有两个相等的实数根；④抛物线与 $\text{[math]}$ 轴的另一个交点是 $\text{[math]}$ ；⑤当 $\text{[math]}$ 时，有 $\text{[math]}$ ；⑥ $\text{[math]}$ ．（m为任意实数）其中正确的是（）

A . ①③⑥ B . ①④⑤ C . ①③⑤ D . ②④⑥

答案解析收藏纠错 + 选题

二、填空题

11. (2020九上·兴城期末) 一元二次方程 $\text{[math]}$ 的根是.

答案解析收藏纠错 + 选题
12. (2021九上·邵阳期末) 某斜坡坡角 $\text{[math]}$ 的正弦值 $\text{[math]}$ ，则该斜坡的坡度为．

答案解析收藏纠错 + 选题
13. (2022九下·定陶期中) 二次函数 $\text{[math]}$ 的顶点坐标是．

答案解析收藏纠错 + 选题
14. (2020九上·成都月考) 如图，正方形 $\text{[math]}$ 中， $\text{[math]}$ ，点 $\text{[math]}$ 为对角线 $\text{[math]}$ 上的动点，以 $\text{[math]}$ 为边作正方形 $\text{[math]}$ ．点 $\text{[math]}$ 是 $\text{[math]}$ 上一点，且 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 度，运动变化过程中， $\text{[math]}$ 的最小值为．

答案解析收藏纠错 + 选题
15. (2024九下·自贡月考) 已知 $\text{[math]}$ ，且 $\text{[math]}$ ，则 $\text{[math]}$ 的值为．

答案解析收藏纠错 + 选题
16. (2020九上·成都月考) 已知 $\text{[math]}$ ， $\text{[math]}$ 是一元二次方程 $\text{[math]}$ 的两实根，且 $\text{[math]}$ ，则 $\text{[math]}$ 的值是．

答案解析收藏纠错 + 选题
17. (2020九上·成都月考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，垂足为 $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 的中点， $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ，则 $\text{[math]}$ 的长为．

答案解析收藏纠错 + 选题
18. 如图，四边形 $\text{[math]}$ 是一张正方形纸片，其面积为 $\text{[math]}$ ．分别在边 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 上顺次截取 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．分别以 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为轴将纸片向内翻折，得到四边形 $\text{[math]}$ ，若四边形 $\text{[math]}$ 的面积为 $\text{[math]}$ ，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
19. (2021八下·拱墅期末) 在平面直角坐标系xOy中，对于不在坐标轴上的任意一点P(x，y)，我们把点P′ $\text{[math]}$ 称为点P的“倒影点”．直线y＝－x＋1上有两点A，B，它们的“倒影点”A′，B′均在反比例函数y＝ $\text{[math]}$ 的图象上．若AB＝2 $\text{[math]}$ ，则k＝．

答案解析收藏纠错 + 选题

三、解答题

20. (2020九上·成都月考)
1. （1）计算 $\text{[math]}$ ；
2. （2）解方程： $\text{[math]}$ ．
答案解析收藏纠错 + 选题
21. (2020九上·成都月考) 先化简，再求值： $\text{[math]}$ ，其中 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
22. (2020九上·成都月考) 为落实我市关于开展中小学课后服务工作的要求，某学校开设了四门校本课程供学生选择：A．趣味数学；B．博乐阅读；C．快乐英语；D．硬笔书法．某年级共有100名学生选择了A课程，为了解本年级选择A课程学生的学习情况，从这100名学生中随机抽取了30名学生进行测试，将他们的成绩（百分制）分成六组，绘制成频数分布直方图．
1. （1）已知70≤x＜80这组的数据为：72，73，74，75，76，76，79．则这组数据的中位数是；众数是；
2. （2）根据题中信息，估计该年级选择A课程学生成绩在80≤x＜90的总人数；
3. （3）该年级学生小乔随机选取了一门课程，则小乔选中课程D的概率是；
4. （4）该年级每名学生选两门不同的课程，小张和小王在选课程的过程中，若第一次都选了课程C，那么他俩第二次同时选择课程A或课程B的概率是多少？请用列表法或树状图的方法加以说明．
答案解析收藏纠错 + 选题

23. (2020九上·平度期末) 为了测量一条两岸平行的河流宽度，三个数学研究小组设计了不同的方案，他们在河南岸的点A处测得河北岸的树H恰好在A的正北方向．测量方案与数据如下表：

课题	测量河流宽度
测量工具	测量角度的仪器，皮尺等
测量小组	第一小组	第二小组	第三小组
测量方案示意图
说明	点B，C在点A的正东方向	点B，D在点A的正东方向	点B在点A的正东方向，点C在点A的正西方向．
测量数据	BC＝60m， ∠ABH＝70°， ∠ACH＝35°．	BD＝20m， ∠ABH＝70°， ∠BCD＝35°．	BC＝101m， ∠ABH＝70°， ∠ACH＝35°．

（1）哪个小组的数据无法计算出河宽？
（2）请选择其中一个方案及其数据求出河宽（精确到0.1m）．（参考数据：sin70°≈0.94，sin35°≈0.57，tan70°≈2.75，tan35°≈0.70）

答案解析收藏纠错 + 选题

24. (2020九上·成都月考) 如图，一次函数 $\text{[math]}$ 与反比例函数 $\text{[math]}$ 的图象交于点 $\text{[math]}$ ， $\text{[math]}$ 两点．与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ．
1. （1）求一次函数的表达式；
2. （2）若点 $\text{[math]}$ 在 $\text{[math]}$ 轴上，且 $\text{[math]}$ 的面积为8，求点 $\text{[math]}$ 的坐标．
3. （3）结合图形，直接写出 $\text{[math]}$ 时 $\text{[math]}$ 的取值范围．
答案解析收藏纠错 + 选题
25. (2020九上·成都月考) 如图，正方形 $\text{[math]}$ 的边长为4，点 $\text{[math]}$ ， $\text{[math]}$ 分别在边 $\text{[math]}$ ， $\text{[math]}$ 上，且 $\text{[math]}$ ， $\text{[math]}$ 的延长线交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ， $\text{[math]}$ 的延长线交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）填空： $\text{[math]}$ $\text{[math]}$ ；（填“>”或“<”或“=”）
2. （2）线段 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 什么关系？请说明理由；
3. （3）当 $\text{[math]}$ 是等腰三角形时，求 $\text{[math]}$ 的长．
答案解析收藏纠错 + 选题
26. (2020九上·成都月考) 某商场试销一种成本为 $\text{[math]}$ 元/件的T 恤，规定试销期间单价不低于成本单价，又获利不得高于 $\text{[math]}$ ，经试销发现，销售量 $\text{[math]}$ （件）与销售单价 $\text{[math]}$ （元/件）符合一次函数 $\text{[math]}$ ，且 $\text{[math]}$ 时， $\text{[math]}$ ； $\text{[math]}$ 时， $\text{[math]}$ .
1. （1）写出销售单价 $\text{[math]}$ 的取值范围；
2. （2）求出一次函数 $\text{[math]}$ 的解析式；
3. （3）若该商场获得利润为 $\text{[math]}$ 元，试写出利润 $\text{[math]}$ 与销售单价 $\text{[math]}$ 之间的关系式，销售单价定为多少时，商场可获得最大利润，最大利润是多少？
答案解析收藏纠错 + 选题
27. (2020九上·成都月考) 如图，点B在线段AC上，点D、E在AC同侧，∠A=∠C=90°，BD⊥BE，AD=BC．
1. （1）求证：AC=AD+CE；
2. （2）若AD=3，CE=5，点P为线段AB上的动点，连接DP，作PQ⊥DP，交直线BE于点Q；
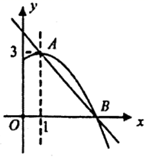
  （i）当点P与A、B两点不重合时，求 $\text{[math]}$ 的值；
  （ii）当点P从A点运动到AC的中点时，求线段DQ的中点所经过的路径（线段）长．（直接写出结果，不必写出解答过程）
答案解析收藏纠错 + 选题
28. (2020九上·成都月考) 如图，抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于 $\text{[math]}$ 、 $\text{[math]}$ 两点，且 $\text{[math]}$ ，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，抛物线对称轴为直线 $\text{[math]}$ ， $\text{[math]}$ 为第一象限内抛物线上一动点，过点 $\text{[math]}$ 作 $\text{[math]}$ 于点 $\text{[math]}$ ，与 $\text{[math]}$ 交于点 $\text{[math]}$ ，设点 $\text{[math]}$ 的横坐标为 $\text{[math]}$ ．
1. （1）求点 $\text{[math]}$ 的坐标与抛物线的表达式：
2. （2）连接 $\text{[math]}$ ， $\text{[math]}$ ，设四边形 $\text{[math]}$ 的面积为 $\text{[math]}$ ．
  ①求 $\text{[math]}$ 与 $\text{[math]}$ 的关系式；
  
  ②当 $\text{[math]}$ 最大时；求 $\text{[math]}$ 点的坐标：
3. （3）若点 $\text{[math]}$ 是对称轴上一点，当 $\text{[math]}$ 时，求 $\text{[math]}$ 的值．
答案解析收藏纠错 + 选题