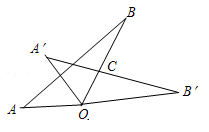
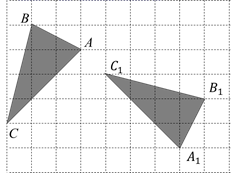
可以由
绕点B逆时针旋转
得到;
点O与
的距离为4;
;
;
.
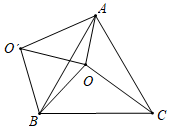
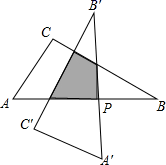

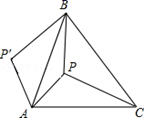
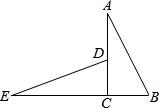
如图1, 中分别以
为边向外作等腰
和等腰
,使
,
,
,连结
,试猜想
与
的大小关系,并说明理由.
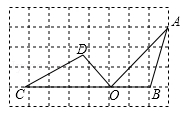
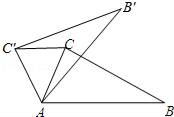
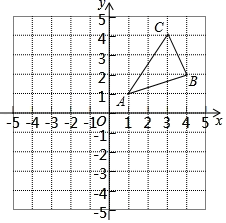
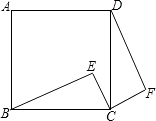
如图2, 中分别以
为边向外作等腰
和等腰
,
,连结
,若
,求
的长.
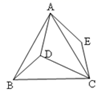
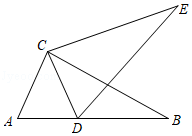
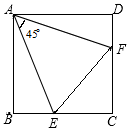
如图3,四边形 中,连结
,
,
,
,
,
,请直接写出
的长.