山西省吕梁市兴县2019-2020学年八年级下学期数学期中试...

更新时间：2021-04-13 浏览次数：139 类型：期中考试

一、单选题

1. (2021八下·越秀期中) 下列根式中，不是最简二次根式的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2020八下·兴县期中) 计算： $\text{[math]}$ ﹣ $\text{[math]}$ 的结果是（　　）

A . $\text{[math]}$ B . 2 $\text{[math]}$ C . $\text{[math]}$ D . 2 $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021八下·营口月考) 如图，正方形ABCD的面积是（）

A . 5 B . 25 C . 7 D . 1

答案解析收藏纠错 + 选题
4. (2024八下·邕宁期中) 如图，菱形 $\text{[math]}$ 中， $\text{[math]}$ ，则 $\text{[math]}$ （）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2022八下·盂县期中) 在平面直角坐标系中， ▱ABCD的顶点A（0，0），B（5，0），D（2，3），则顶点C的坐标是（）

A . （3，7） B . （5，3） C . （7，3） D . （8，2）

答案解析收藏纠错 + 选题
6. (2022·常州) 如图，在△ABC中，D ， E分别是AB ， AC边的中点，若DE＝2，则BC的长度是（　　）

A . 6 B . 5 C . 4 D . 3

答案解析收藏纠错 + 选题
7. (2020八下·兴县期中) 下列说法错误的是（）

A . 平行四边形对边平行 B . 两组对边平行的四边形是平行四边形 C . 平行四边形对角相等 D . 一组对角相等的四边形是平行四边形

答案解析收藏纠错 + 选题
8. (2020八下·兴县期中) 如图，在平面直角坐标系中，点P坐标为（﹣2，3），以点O为圆心，以OP的长为半径画弧，交x轴的负半轴于点A，则点A的横坐标为（　　）

A . $\text{[math]}$ B . 2﹣ $\text{[math]}$ C . ﹣ $\text{[math]}$ D . $\text{[math]}$ ﹣2

答案解析收藏纠错 + 选题
9. (2020八下·兴县期中) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，D为边 $\text{[math]}$ 上一动点， $\text{[math]}$ 于点E， $\text{[math]}$ 于点F，则 $\text{[math]}$ 的最小值为（）

A . 2.4 B . 3 C . 4.8 D . 5

答案解析收藏纠错 + 选题
10. (2022八下·铜官期末) 勾股定理是人类最伟大的科学发现之一，在我国古算书《周髀算经》中早有记载。如图1，以直角三角形的各边为边分别向外作正方形，再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积，则一定能求出（）

A . 直角三角形的面积 B . 最大正方形的面积 C . 较小两个正方形重叠部分的面积 D . 最大正方形与直角三角形的面积和

答案解析收藏纠错 + 选题

二、填空题

11. (2022九下·安岳开学考) 代数式 $\text{[math]}$ 有意义时，x应满足的条件是．

答案解析收藏纠错 + 选题
12. (2020八下·兴县期中) 一个三角形的一边长为 $\text{[math]}$ ，这条边上的高为 $\text{[math]}$ ，则这个三角形的面积为 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
13. (2020八下·兴县期中) 在菱形 $\text{[math]}$ 中，对角线 $\text{[math]}$ 、 $\text{[math]}$ 交于点 $\text{[math]}$ ，点 $\text{[math]}$ 为 $\text{[math]}$ 中点，过点 $\text{[math]}$ 作 $\text{[math]}$ 于点 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ ，若 $\text{[math]}$ 则 $\text{[math]}$ °.

答案解析收藏纠错 + 选题
14. (2020八下·兴县期中) 如图，用6个边长为l的小正方形构造的网格图，角 $\text{[math]}$ ， $\text{[math]}$ 的顶点均在格点上，则 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
15. (2020八下·兴县期中) 如图，在正方形 $\text{[math]}$ 中， $\text{[math]}$ ，点E在正方形 $\text{[math]}$ 的边上，若 $\text{[math]}$ ，则线段 $\text{[math]}$ 的长为．

答案解析收藏纠错 + 选题

三、解答题

16. (2020八下·兴县期中) 计算题.
1. （1） $\text{[math]}$
2. （2） $\text{[math]}$
答案解析收藏纠错 + 选题
17. (2020八下·兴县期中) 为了打赢湖北保卫战、武汉保卫战，4万多名医护人员逆行出征，约4万名建设者从八方赶来，并肩奋战，抢建火神山和雷神山医院．他们日夜鏖战，与病毒竞速，创造了10天左右时间建成两座传染病医院的“中国速度”！他们不畏风险，同困难斗争，充分展现团结起来打硬仗的“中国力量”，在建设过程中，有一位木工遇到了这样一道数学题：
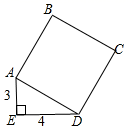
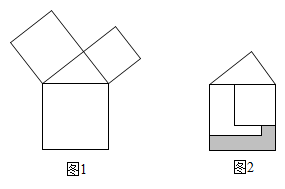
有一块矩形木板，木工采用如图的方式，在木板上截出两个面积分别为 $\text{[math]}$ 和 $\text{[math]}$ 的正方形木板．
1. （1）求剩余木料的面积？
2. （2）如果木工想从剩余的木料中截出长为 $\text{[math]}$ ，宽为 $\text{[math]}$ 的长方形木条，最多能截出块这样的木条．
答案解析收藏纠错 + 选题
18. (2020八下·兴县期中) 菱形 $\text{[math]}$ 中， $\text{[math]}$ 于点E，且 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求 $\text{[math]}$ 的长；
2. （2）求菱形 $\text{[math]}$ 的面积．
答案解析收藏纠错 + 选题
19. (2020八下·兴县期中) 有一架秋千，当它静止时，踏板离地的垂直高度DE＝1m ，将它往前推送6m（水平距离BC＝6m）时，秋千的踏板离地的垂直高度BF＝4m ，秋千的绳索始终拉得很直，求绳索AD的长度．

答案解析收藏纠错 + 选题
20. (2020八下·兴县期中)
1. （1）正方形网格中，每个小正方形的顶点称为格点，以格点为顶点的三角形叫做格点三角形，在图1正方形网格（每个小正方形边长为1）中画出格点△ABC，使AB=AC=5，BC= $\text{[math]}$
2. （2）在△ABC中， AB、BC、AC三边的长分别为 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ，求这个三角形的面积．小华同学在解答这道题时，先画一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），如图2所示．这样不需求△ABC的高，而借用网格就能计算出它的面积．这种方法叫做构图法．
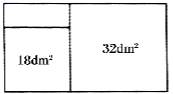
  ①△ABC的面积为：．
  
  ②若△DEF三边的长分别为 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ ，请在图3的正方形网格中画出相应的△DEF，并利用构图法求出它的面积为．
答案解析收藏纠错 + 选题
21. (2024八下·澧县期中) 已知：如图，平行四边形ABCD中，M、N分别为AB和CD的中点.
1. （1）求证：四边形AMCN是平行四边形；
2. （2）若AC＝BC＝5，AB＝6，求四边形AMCN的面积.
答案解析收藏纠错 + 选题
22. (2022八下·广陵期中) 阅读下面材料：
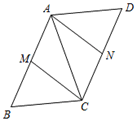
在数学课上，老师请同学思考如下问题：如图1，我们把一个四边形ABCD的四边中点E，F，G，H依次连接起来得到的四边形EFGH是平行四边形吗.

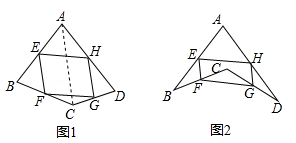
小敏在思考问题时，有如下思路：连接AC.

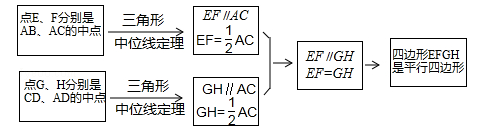
结合小敏的思路作答：
1. （1）若只改变图1中四边形ABCD的形状（如图2），则四边形EFGH还是平行四边形吗？说明理由，参考小敏思考问题的方法解决一下问题；
2. （2）如图2，在（1）的条件下，若连接AC，BD.
  ①当AC与BD满足什么条件时，四边形EFGH是菱形，写出结论并证明；
  
  ②当AC与BD满足什么条件时，四边形EFGH是矩形，直接写出结论.
答案解析收藏纠错 + 选题
23. (2020八下·兴县期中) 综合与实践：折纸中的数学

问题背景

在数学活动课上，老师首先将平行四边形纸片ABCD按如图①所示方式折叠，使点C与点A重合，点D落到D′处，折痕为EF ．这时同学们很快证得：△AEF是等腰三角形．接下来各学习小组也动手操作起来，请你解决他们提出的问题．

操作发现
1. （1） “争先”小组将矩形纸片ABCD按上述方式折叠，如图②，发现重叠部分△AEF恰好是等边三角形，求矩形ABCD的长、宽之比是多少？
2. （2）实践探究
  “励志”小组将矩形纸片ABCD沿EF折叠，如图③，使B点落在AD边上的B′处；沿B′G折叠，使D点落在D′处，且B′D′过F点．试探究四边形EFGB′是什么特殊四边形？
3. （3）再探究：在图③中连接BB′，试判断并证明△BB′G的形状．
答案解析收藏纠错 + 选题