四川省凉山州2021年数学中考一模试卷

更新时间：2021-05-20 浏览次数：207 类型：中考模拟

一、单选题

1. (2023八上·鲤城期中) 下列各数中，属于无理数的是（）

A . $\text{[math]}$ B . 1.414 C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2023七下·界首期末) 如图，将一块含有30°角的直角三角板的两个顶点分别放在直尺的两条平行对边上，若∠α=135°，则∠β等于（）

A . 45° B . 60° C . 75° D . 85°

答案解析收藏纠错 + 选题
3. (2023七上·文登期中) 下面四个图形中，属于轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2021·四川模拟) 如图，已知 $\text{[math]}$ ，以 $\text{[math]}$ 两点为圆心，大于 $\text{[math]}$ 的长为半径画圆弧，两弧相交于点 $\text{[math]}$ ，连接 $\text{[math]}$ 与 $\text{[math]}$ 相交于点 $\text{[math]}$ ，则 $\text{[math]}$ 的周长为（）

A . 8 B . 9 C . 11 D . 13

答案解析收藏纠错 + 选题
5. (2021·四川模拟) 下列运算正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2021·四川模拟) 下列多项式中，在实数范围不能分解因式的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
7. (2021·四川模拟) 已知 $\text{[math]}$ 是方程 $\text{[math]}$ 的根，那么代数式 $\text{[math]}$ 的值是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ 或 $\text{[math]}$ D . $\text{[math]}$ 或 $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2021·迁安模拟) 一名射箭运动员统计了45次射箭的成绩，并绘制了如图所示的折线统计图则在射箭成绩的这组数据中，众数和中位数分别是（）

A . 18，8 B . 8，8 C . 8，9 D . 18，18

答案解析收藏纠错 + 选题
9. (2021·四川模拟) 下列说法正确的是（）
①斜边中线和一个锐角分别对应相等的两个直角三角形全等；②一个图形和它经过平移所得的图形中，各组对应点所连接的线段平行且相等；③通常温度降到 $\text{[math]}$ 以下，纯净的水会结冰是随机事件；④一个角的两边与另一个角的两边分别平行，那么这两个角相等；⑤在同一平面内，过一点有且只有一条直线与已知直线垂直；

A . ①③ B . ②④ C . ③④ D . ①⑤

答案解析收藏纠错 + 选题
10. (2022九下·安岳开学考) 如图，某地修建高速公路，要从A地向B地修一条隧道（点A，B在同一水平面上）．为了测量A，B两地之间的距离，一架直升飞机从A地出发，垂直上升800米到达C处，在C处观察B地的俯角为α，则A，B两地之间的距离为（）

A . 800sinα米 B . 800tanα米 C . $\text{[math]}$ 米 D . $\text{[math]}$ 米

答案解析收藏纠错 + 选题
11. (2021九上·南雄期末) 如图，△ABC的内切圆⊙O与BC，CA，AB分别相切于点D，E，F，且AB＝5，BC＝13，CA＝12，则阴影部分(即四边形AEOF)的面积是（）

A . 4 B . 6.25 C . 7.5 D . 9

答案解析收藏纠错 + 选题
12. (2021·四川模拟) 已知抛物线 $\text{[math]}$ 的对称轴为直线 $\text{[math]}$ ，与 $\text{[math]}$ 轴的一个交点坐标为 $\text{[math]}$ ，其部分图象如图所示，下列结论：
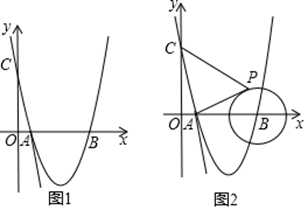
①抛物线过原点；② $\text{[math]}$ ；③ $\text{[math]}$ ；④抛物线的顶点坐标为 $\text{[math]}$ ；⑤当 $\text{[math]}$ 时， $\text{[math]}$ 随 $\text{[math]}$ 增大而增大.其中结论正确的是（）

A . ①②③ B . ③④⑤ C . ①③④ D . ①④⑤

答案解析收藏纠错 + 选题

二、填空题

13. (2021·四川模拟) 若式子 $\text{[math]}$ 有意义，则x的取值范围是．

答案解析收藏纠错 + 选题
14. (2021·四川模拟) 已知射线 $\text{[math]}$ ，从 $\text{[math]}$ 点再引射线 $\text{[math]}$ ， $\text{[math]}$ ，使 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的度数为.

答案解析收藏纠错 + 选题
15. (2021·四川模拟) 如图，在平面直角坐标系中，点A在第一象限，⊙A与 $\text{[math]}$ 轴相切于B，与 $\text{[math]}$ 轴交于C（0，1）、D（0，4）两点，则点A的坐标是.

答案解析收藏纠错 + 选题
16. (2021·四川模拟)
如图，在⊙O中，CD是直径，弦AB⊥CD，垂足为E，连接BC．若AB= $\text{[math]}$ ， ∠BCD=30°，则⊙O的半径为．

答案解析收藏纠错 + 选题
17. (2021·四川模拟) 背面完全一样的四张卡片上分别写有数字2、5、0、3，从中任取一张，并用这张卡片上的数字与1的差作为k值，抽到能使一元二次方程 $\text{[math]}$ 有解的卡片概率是.

答案解析收藏纠错 + 选题
18. (2021·四川模拟) 已知 $\text{[math]}$ ，则代数式 $\text{[math]}$ 的值为.

答案解析收藏纠错 + 选题
19. (2021·四川模拟) 如图，在平面直角坐标系中，将正方形 $\text{[math]}$ 绕点 $\text{[math]}$ 逆时针旋转 $\text{[math]}$ 后得到正方形 $\text{[math]}$ ，依此方式，绕点 $\text{[math]}$ 连续旋转2020次得到正方形 $\text{[math]}$ ，如果点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，那么点 $\text{[math]}$ 的坐标为.

答案解析收藏纠错 + 选题

三、解答题

20. (2023·双柏模拟) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
21. (2023九上·渠县期中) 先化简，再求值：（1+ $\text{[math]}$ ）÷ $\text{[math]}$ ，其中x是不等式组 $\text{[math]}$ 的整数解．

答案解析收藏纠错 + 选题
22. (2021·四川模拟) 如图， $\text{[math]}$ 为矩形 $\text{[math]}$ 的对角线，将边 $\text{[math]}$ 沿 $\text{[math]}$ 折叠，使点 $\text{[math]}$ 落在 $\text{[math]}$ 上的点 $\text{[math]}$ 处，将边 $\text{[math]}$ 沿 $\text{[math]}$ 折叠，使点 $\text{[math]}$ 落在 $\text{[math]}$ 上的点 $\text{[math]}$ 处.
1. （1）求证： $\text{[math]}$ ；
2. （2）若 $\text{[math]}$ ，求四边形 $\text{[math]}$ 的面积.
答案解析收藏纠错 + 选题
23. (2022七上·青原期末) 在国务院办公厅发布《中国足球发展改革总体方案》之后，某校为了调查本校学生对足球知识的了解程度，随机抽取了部分学生进行一次问卷调查，并根据调查结果绘制了如图的统计图，请根据图中所给的信息，解答下列问题：
1. （1）本次接受问卷调查的学生总人数是；
2. （2）补全折线统计图．
3. （3）扇形统计图中，“了解”所对应扇形的圆心角的度数为，m的值为
4. （4）若该校共有学生3000名，请根据上述调查结果估算该校学生对足球的了解程度为“不了解”的人数．
答案解析收藏纠错 + 选题
24. (2021·四川模拟) 如图，在平面直角坐标系中，一次函数 $\text{[math]}$ 的图象与反比例函数 $\text{[math]}$ 的图象相交于第一、三象限内的 $\text{[math]}$ 两点，与 $\text{[math]}$ 轴交于点 $\text{[math]}$ .
1. （1）求该反比例函数和一次函数的解析式；
2. （2）在y轴上找一点P使 $\text{[math]}$ 最大，求 $\text{[math]}$ 的最大值及点P的坐标；
答案解析收藏纠错 + 选题
25. (2022·莘县模拟) 如图，AB、AC分别是⊙O的直径和弦，OD⊥AC于点D，过点A作⊙O的切线与OD的延长线交于点P，PC、AB的延长线交于点F.
1. （1）求证：PC是⊙O的切线；
2. （2）若∠ABC=60°，AB=10，求线段CF的长，
答案解析收藏纠错 + 选题
26. (2021·四川模拟) 我们知道，有理数包括整数、有限小数和无限循环小数，事实上，所有的有理数都可以化为分数形式（整数可看作分母为1的分数），那么无限循环小数如何表示为分数形式呢？请看以下示例：
例：将 $\text{[math]}$ 化为分数形式

由于 $\text{[math]}$ =0.777…，设x=0.777…①

则10x=7.777…②

②﹣①得9x=7，解得x= $\text{[math]}$ ，于是得 $\text{[math]}$ = $\text{[math]}$ .

同理可得 $\text{[math]}$ = $\text{[math]}$ ， $\text{[math]}$ =1+ $\text{[math]}$ =1+ $\text{[math]}$ ，

根据以上阅读，回答下列问题：（以下计算结果均用最简分数表示）
1. （1）（基础训练）
  $\text{[math]}$ =， $\text{[math]}$ =；
2. （2）将 $\text{[math]}$ 化为分数形式，写出推导过程；
3. （3）（能力提升）
  $\text{[math]}$ =， $\text{[math]}$ =；
  
  （注： $\text{[math]}$ =0.315315…， $\text{[math]}$ =2.01818…）
4. （4）（探索发现）
  ①试比较 $\text{[math]}$ 与1的大小： $\text{[math]}$ 1（填“＞”、“＜”或“=”）
  
  ②若已知 $\text{[math]}$ = $\text{[math]}$ ，则 $\text{[math]}$ =.
  
  （注： $\text{[math]}$ =0.285714285714…）
答案解析收藏纠错 + 选题
27. (2021·四川模拟) 我州拥有充足的日照、优质的水源和土壤，非常利于冬草莓种植，但草莓的产量对培育技术要求很高.某基地为降低成本、提高产量，发现基地草莓的生长率 $\text{[math]}$ 与温度 $\text{[math]}$ 有如下关系：如图，当 $\text{[math]}$ 时可近似用函数 $\text{[math]}$ 刻画；当 $\text{[math]}$ 时可近似用函数 $\text{[math]}$ 刻画.按照经验，基地草莓提前上市的天数 $\text{[math]}$ （天）与生长率 $\text{[math]}$ 之间满足已学过的函数关系，部分数据如下：

生长率 $\text{[math]}$

0.2

0.25

0.3

0.35

提前上市的天数 $\text{[math]}$ （天）

0

5

10

15
1. （1）求 $\text{[math]}$ 的值；
2. （2）写出 $\text{[math]}$ 关于 $\text{[math]}$ 的函数表达式；
3. （3）用含 $\text{[math]}$ 的代数式表示 $\text{[math]}$ ；
4. （4）天气寒冷，大棚加温可改变草莓生长速度.大棚恒温 $\text{[math]}$ 时每天的成本为100元，计划该作物30天后上市，现根据市场调査：每提前一天上市售出（一次售完），销售额可增加600元.因此决定给大棚继续加温，但加温导致成本增加，估测加温到 $\text{[math]}$ 时的成本为200元/天，但若欲加温到 $\text{[math]}$ ，由于要采用特殊方法，成本增加到400元/天.问加温到多少度时增加的利润最大？并说明理由.（注：假如草莓上市售出后大棚暂停使用）
答案解析收藏纠错 + 选题
28. (2021·四川模拟) 如图1，在平面直角坐标系中，直线y＝﹣5x+5与x轴，y轴分别交于A，C两点，抛物线y＝x²+bx+c经过A，C两点，与x轴的另一交点为B
1. （1）求抛物线解析式及B点坐标；
2. （2）若点M为x轴下方抛物线上一动点，连接MA、MB、BC，当点M运动到某一位置时，四边形AMBC面积最大，求此时点M的坐标及四边形AMBC的面积；
3. （3）如图2，若P点是半径为2的⊙B上一动点，连接PC、PA，当点P运动到某一位置时，PC+ $\text{[math]}$ PA的值最小，请求出这个最小值，并说明理由.
答案解析收藏纠错 + 选题