 B .
B . 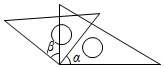 C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 


|
射击次数( | 10 | 20 | 50 | 100 | 200 | 500 | … |
| 击中靶心次数( | 8 | 17 | 45 | 92 | 182 | 453 | … |
| 击中靶心频率( | 0.80 | 0.85 | 0.90 | 0.92 | 0.91 | 0.905 | … |
由此表估计这个射手射击1次,击中靶心的概率是.(保留一位小数)
①作 的角平分线交
于点E;
②作线段 的垂直平分线交
于点F.

|
次数 |
1 |
2 |
3 |
4 |
5 |
|
小明 |
13.3 |
13.4 |
13.3 |
|
13.3 |
|
小亮 |
13.2 |
|
13.1 |
13.5 |
13.3 |
|
x |
… |
﹣4 |
﹣3 |
﹣2 |
﹣1 |
﹣ | 0 | | 1 | 2 | 3 | 4 | … |
| y | … | 5 | 0 | ﹣3 | ﹣4 | ﹣ | ﹣3 | ﹣ | ﹣4 | ﹣3 | 0 | 5 | … |
小京根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小京的探究过程,请补充完整:

①x= 对应的函数值y约为;
②该函数的一条性质:.


如图2,等腰直角三角形ABC中,∠ABC=90°,AB=BC,点G,H在边AC上,且∠GBH=45°,写出图中线段AG,GH,CH之间的数量关系并证明.