

解:因为∠1=∠2(已知),
所以// ,
所以∠E+∠=180°
因为AD//BE(已知),
所以∠A+∠=180°
所以∠A=∠E

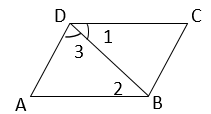
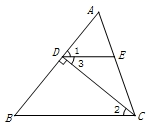
证明:∵()
∴∠CDA=90°,∠DAB=90°().
∴∠4+∠3=90°,∠2+∠1=90°.
又∵∠1=∠4,
∴(),
∴DF∥AE().
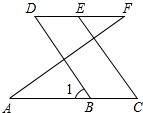
解:∵∠A=∠F(),
∴AC∥DF(),
∴∠D=∠1(),
又∵∠C=∠D(),
∴∠1=∠C(),
∴BD∥CE().
请在括号内填写出证明依据.
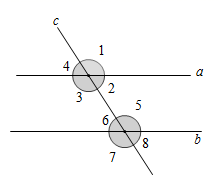
证明:∵ (已知)
∴ ()
∵ ()
∴ ()
∴ ∥
()
∴ ()
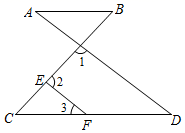
如图,∠1+∠2=180°,∠3=∠A .
求证:∠B=∠C .
证明:∵∠1+∠2=180°,
∴(同旁内角互补,两直线平行).
∴∠3=∠D().
又∵∠3=∠A ,
∴.
∴AB∥CD().
∴∠B=∠C().
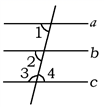
求证:∠1+∠3 = 180°

证明:∵ AB∥CD(已知),
∴ ∠1+∠2 = 180°()
又∵ ∠2 = ∠3()
∴ ∠1+∠3=180°()
求证:∠2 = ∠C .
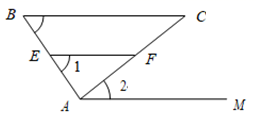
证明:∵ ∠1 = ∠B(已知),
∴ EF∥BC()
∵ AM∥EF(已知),
∴ AM∥BC()
∴ ∠2 = ∠C()


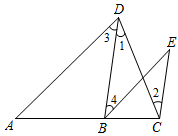

证明:∵∠DAF=∠F ( ▲ )
∴ ▲ ∥ ▲ ( ▲ )
∴∠D=∠DCF ( ▲ )
∵∠B=∠D( ▲ )
∴∠ ▲ =∠DCF (等量代换)
∴AB∥DC ( ▲ )

求证:
证明:理由如下:
平分
(已知)
(已知)
(等量代换)
又 (已知)
(等量代换)
