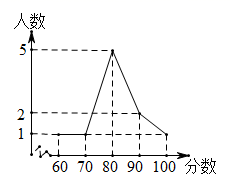
|
A |
B |
C |
D |
E |
|
|
甲 |
90 |
92 |
94 |
95 |
88 |
|
乙 |
89 |
86 |
87 |
94 |
91 |

规定:演讲答辩得分按“去掉一个最高分和一个最低分再算平均分”的方法确定;民主测评得分=“好”票数×2分+“较好“票数×1分+“一般”票数×0分.
收集数据
从八、九两个年级各随机抽取20名学生,进行了体质健康测试,测试成绩(百分制)如下:
|
八年级 |
78 |
86 |
74 |
81 |
75 |
76 |
87 |
70 |
75 |
90 |
|
75 |
79 |
81 |
70 |
74 |
80 |
86 |
69 |
83 |
77 |
|
|
九年级 |
93 |
73 |
88 |
81 |
72 |
81 |
94 |
83 |
77 |
83 |
|
80 |
81 |
70 |
81 |
73 |
78 |
82 |
80 |
70 |
40 |
整理、描述数据
按如下分数段整理、描述 这两组样本数据:
|
成绩 人数x 部门 |
40≤x≤49 |
50≤x≤59 |
60≤x≤69 |
70≤x≤79 |
80≤x≤89 |
90≤x≤100 |
|
八年级 |
0 |
0 |
1 |
11 |
|
1 |
|
九年级 |
1 |
0 |
0 |
7 |
|
(说明:成绩80分及以上为体质健康优秀,70~79分为体质健康良好,60~69分为体质健康合格,60分以下为体质健康不合格)
分析数据
两组样本数据的平均数、中位数、众数、方差如下表所示:
|
年级 |
平均数 |
中位数 |
众数 |
方差 |
|
八年级 |
78.3 |
77.5 |
75 |
33.6 |
|
九年级 |
78 |
80.5 |
|
52.1 |
|
A |
B |
C |
D |
E |
F |
|
|
甲 |
89 |
97 |
90 |
93 |
95 |
94 |
|
乙 |
89 |
92 |
90 |
97 |
94 |
94 |

甲:63 70 95 84 75 82 78 78 86 96
92 100 52 89 88 84 84 92 90 84
乙:75 95 85 93 85 92 84 89 96 98
46 86 77 100 100 68 50 85 78 69
整理上面的数据,得到表格如下:
|
测试成绩(分) |
| | | | |
| 甲 | 1 | 2 | 3 | 9 | 5 |
| 乙 | 2 | 2 | 3 | 6 | 7 |
样本数据的平均数、中位数、众数如下表所示:
| 统计量 | 平均数 | 中位数 | 众数 |
| 甲 | 83.1 | m | 84 |
| 乙 | 82.4 | 85.5 | n |
根据以上信息,解答下列问题:

设销售员的月销售额为x(单位:万元).销售部规定:当x<16时为“不称职”,当16≤x<20时为“基本称职”,当20≤x<25时为“称职”,当x≥25时为“优秀”.根据以上信息,解答下列问题:
a.小云所住小区5月1日至30日的厨余垃圾分出量统计图:
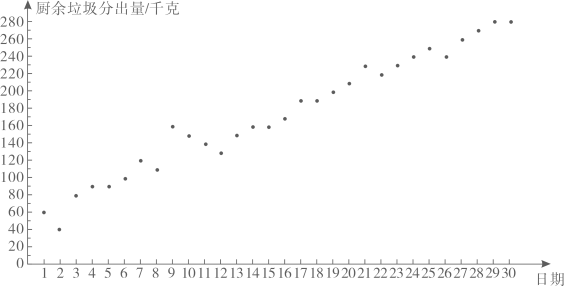
b.小云所住小区5月1日至30日分时段的厨余垃圾分出量的平均数如下:
| 时段 | 1日至10日 | 11日至20日 | 21日至30日 |
| 平均数 | 100 | 170 | 250 |

|
姓名 |
平均数(环) |
众数(环) |
方差 |
|
甲 |
|||
|
乙 |
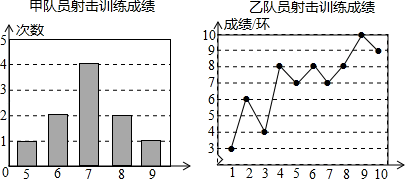
根据以上信息,整理分析数据如下:
| 平均成绩/环 | 中位数/环 | 众数/环 | 方差 | |
| 甲 | a | 7 | 7 | 1.2 |
| 乙 | 7 | b | 8 | c |