浙江省宁波市2021年数学中考复习评估试卷（二）

更新时间：2024-11-06 浏览次数：170 类型：中考模拟

一、单选题

1. (2024·海安模拟) 在﹣ $\text{[math]}$ ，﹣ $\text{[math]}$ ，0，1四个数中，最大的数是（）

A . 1 B . 0 C . ﹣ $\text{[math]}$ D . ﹣ $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2022七下·慈溪期中) 如图①，现有边长为 $\text{[math]}$ 和a+b的正方形纸片各一张，长和宽分别为 $\text{[math]}$ ， $\text{[math]}$ 的长方形纸片一张，其中 $\text{[math]}$ .把纸片Ⅰ，Ⅲ按图②所示的方式放入纸片Ⅱ内，已知图②中阴影部分的面积满足 $\text{[math]}$ ，则 $\text{[math]}$ ， $\text{[math]}$ 满足的关系式为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
3. (2021·宁波模拟) 下列图形中，不是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
4. (2024九下·自贡期中) 我国北斗公司在2020年发布了一款代表国内卫星导航系统最高水平的芯片，该芯片的制造工艺达到了0.000000022米.用科学记数法表示0.000000022为（）

A . 22×10^﹣10 B . 2.2×10^﹣10 C . 2.2×10^﹣9 D . 2.2×10^﹣8

答案解析收藏纠错 + 选题
5. (2021·宁波模拟) 某几何体分别从正面、左面、上面看到的平面图形如图所示，则该几何体是（）

A . 圆柱 B . 圆锥 C . 长方体 D . 球

答案解析收藏纠错 + 选题
6. (2021·宁波模拟) 我市某中学举办了一次以“阳光少年，我们是好伙伴”为主题的演讲比赛，有9名同学参加了决赛，他们的决赛成绩各不相同，其中小辉已经知道自己的成绩，但能否进前5名，他还必须清楚这9名同学成绩的（）

A . 平均数 B . 众数 C . 中位数 D . 方差

答案解析收藏纠错 + 选题
7. (2021·宁波模拟) 在下列命题中：①有一个外角是120°的等腰三角形是等边三角形；②有两个外角相等的等腰三角形是等边三角形；③有一边上的高也是这边上的中线的三角形是等边三角形；④三个外角都相等的三角形是等边三角形．正确的命题有（）

A . 4个 B . 3个 C . 2个 D . 1个

答案解析收藏纠错 + 选题
8. (2021八上·黄埔期末) 如图，已知在△ABC中，CD是AB边上的高线，BE平分∠ABC，交CD于点E，BC=5，DE=2，则△BCE的面积等于（）

A . 10 B . 7 C . 5 D . 4

答案解析收藏纠错 + 选题
9. (2021·宁波模拟) 如图，在纸上剪一个圆形和一个扇形的纸片，使之恰好能围成一个圆锥模型，若圆的半径r＝1，扇形的半径为R，扇形的圆心角等于90°，则R的值是（）

A . R＝2 B . R＝3 C . R＝4 D . R＝5

答案解析收藏纠错 + 选题
10. (2021九上·大石桥期中) 已知二次函数y=kx²-7x-7的图象和x轴有交点，则k的取值范围是（）

A . k>- $\text{[math]}$ B . k>- $\text{[math]}$ 且k≠0 C . k≥- $\text{[math]}$ D . k≥- $\text{[math]}$ 且k≠0

答案解析收藏纠错 + 选题
11. (2023七上·章贡期中) 如图，下列各图形中的三个数之间均具有相同的规律.根据此规律，图形中M与m、n的关系是（）

A . M=mn B . M=n(m+1) C . M=mn+1 D . M=m(n+1)

答案解析收藏纠错 + 选题
12. (2022·高唐模拟) 如图，在正方形ABCD中，AB=6，点Q是AB边上的一个动点（点Q不与点B重合），点M，N分别是DQ，BQ的中点，则线段MN=（）

A . $\text{[math]}$ B . $\text{[math]}$ C . 3 D . 6

答案解析收藏纠错 + 选题

二、填空题

13. (2024九下·重庆市模拟) 化简：a+1+a（a+1）+a（a+1）²+…+a（a+1）⁹⁹=．

答案解析收藏纠错 + 选题
14. (2021·宁波模拟) 关于x的不等式组 $\text{[math]}$ 无整数解，则a的取值范围为.

答案解析收藏纠错 + 选题
15. (2021八下·东阳期末) 已知x为实数，且满足 $\text{[math]}$ ，那么x²+3x=.

答案解析收藏纠错 + 选题
16. (2021·宁波模拟) 如图，一楼房AB后有一假山，其斜面坡度为i＝1： $\text{[math]}$ （斜面坡度是指坡面的铅直高度与水平宽度的比），山坡坡面上点E处有一休息亭，测得假山坡脚C与楼房水平距离BC＝25米，与亭子距离CE＝20米，小丽从楼房顶测得E点的俯角为45°，则楼房AB的高为米.

答案解析收藏纠错 + 选题
17. (2021·宁波模拟) 如图，▱ABCD的两边AB、BC分别切⊙O于点A、C，若∠B＝50°，则∠DAE＝.

答案解析收藏纠错 + 选题
18. (2021·宁波模拟) 在平面直角坐标系中，O为坐标原点，反比例函数y＝ $\text{[math]}$ （k＞0）的图象上有两点A，B（点A在B上方），直线AB的解析式为y＝k'x+18.在第一象限内有一点C（8，12），∠ACB＝90°，若△ABC和△ABO的面积相等.则k的值为.

答案解析收藏纠错 + 选题

三、解答题

19. (2021·宁波模拟) 解答下列各题：
1. （1）计算： $\text{[math]}$ .
2. （2）解方程： $\text{[math]}$ .
答案解析收藏纠错 + 选题
20. (2021·宁波模拟) 图1是由六个全等且边长为2的小正五边形，以及五个全等且顶角为36°、腰长为2的等腰三角形镶嵌而成的一个大正五边形，正五边形和等腰三角形的顶点称为格点，连接格点而成的三角形称为格点三角形.在图2的三个图中，分别画出一个与图中已知△ABC相似但不全等的格点三角形，并注明三角形的顶点字母.

答案解析收藏纠错 + 选题

21. (2021·宁波模拟) 语文教研组为了解我校学生每天课外阅读所用的时间情况，从我校学生中随机抽取了部分学生进行问卷调查，并将结果绘制成如图不完整的频数分布直方图.

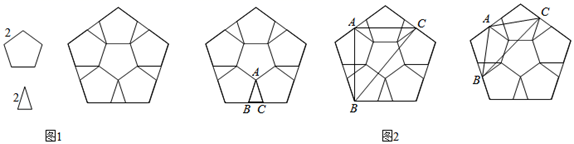
每天课外阅读时间/h	频数	频率
0＜t≤0.5	24
0.5＜t≤1	36	0.3
1＜t≤1.5		0.4
1.5＜t≤2	12	b
合计	a	1

根据以上信息，回答下列问题：

（1）表中a＝，b＝；
（2）请补全频数分布直方图；
（3）我校有学生4800人，请估计我校学生每天课外阅读时间超过1小时的人数.

答案解析收藏纠错 + 选题

22. (2021·宁波模拟) 如图，在▱ABCD中，BC＝2AB＝4，点E，F分别是BC，AD的中点.
1. （1）求证：△ABE≌△CDF；
2. （2）当四边形AECF为菱形时，求出该菱形的面积.
答案解析收藏纠错 + 选题
23. (2021·宁波模拟) 某商店经营一种小商品，进价为40元，据市场调查，销售价是60元时，平均每天销售量是300件，而销售价每降低1元，平均每天就可以多售出20件.
1. （1）假定每件商品降价x元，商店每天销售这种小商品的利润是y元，请写出y与x间的函数关系式；
2. （2）每件小商品销售价是多少元时，商店每天销售这种小商品的利润最大？最大利润是多少？
答案解析收藏纠错 + 选题
24. (2021·宁波模拟) 已知抛物线C₁的解析式为y＝ $\text{[math]}$ x²+ $\text{[math]}$ x+2，抛物线与x轴交于A，B两点（A在B在左边）与y轴于C点.
1. （1）求点A、B、C的坐标；
2. （2）将抛物线C₁平移得到抛物线C₂ ，且C₂经过C₁上一点P（2，m）C₂交y轴于Q，当PQ与y轴相交所成的锐角为45°时，求C₂的解析式；
3. （3）将抛物线C₁沿直线BC平移，与射线AC仅有一个公共点，求抛物线顶点横坐标的取值或取值范围.
答案解析收藏纠错 + 选题
25. (2021·宁波模拟) 阅读以下材料，并按要求完成相应的任务.如图（1），已知四边形ABCD的对角线AC，BD相交于点O，点M是BC边的中点，过点M作ME∥AC交BD于点E，作MF∥BD交AC于点F.我们称四边形0EMF为四边形ABCD的“伴随四边形”.
1. （1）若四边形ABCD是菱形，则其“伴随四边形”是，若四边形ABCD矩形，则其“伴随四边形”是：（在横线上填特殊平行四边形的名称）
2. （2）如图（2），若四边形ABCD是矩形，M是BC延长线上的一个动点，其他条件不变，点F落在AC的延长线上，请写出线段OB、ME，MF之间的数量关系，并说明理由.
答案解析收藏纠错 + 选题
26. (2021·宁波模拟) 如图
1. （1）（学习心得）
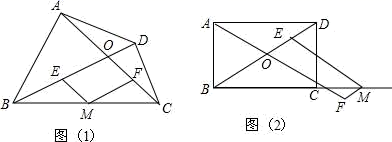
  于彤同学在学习完“圆”这一章内容后，感觉到一些几何问题如果添加辅助圆，运用圆的知识解决，可以使问题变得非常容易.
  
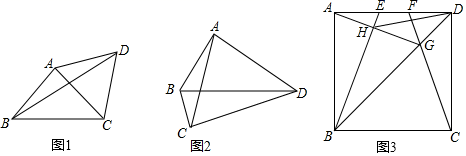
  例如：如图1，在△ABC中，AB＝AC，∠BAC＝90°，D是△ABC外一点，且AD＝AC，求∠BDC的度数.若以点A为圆心，AB为半径作辅助⊙A，则点C、D必在⊙A上，∠BAC是⊙A的圆心角，而∠BDC是圆周角，从而可容易得到∠BDC＝°.
2. （2）（问题解决）
  如图2，在四边形ABCD中，∠BAD＝∠BCD＝90°，∠BDC＝25°，求∠BAC的度数.
3. （3）（问题拓展）
  如图3，如图，E，F是正方形ABCD的边AD上两个动点，满足AE＝DF.连接CF交BD于点G，连接BE交AG于点H.若正方形的边长为2，则线段DH长度的最小值是.
答案解析收藏纠错 + 选题