B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 

①该函数的定义域为 ;
②该函数与x轴没有交点;
③该函数与y轴交于点 ;
④若 是该函数上两点,当
时,一定有
.


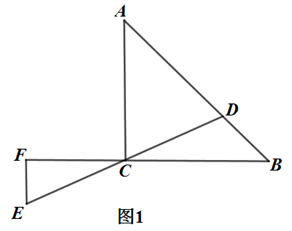
求作: ,使得
,
作法:①在射线 上取点
,以点
为圆心,
长为半径画圆,交射线
于点
;
②连接
③以点 为圆心,
长为半径画弧,交射线
于点
;连接
线段 就是所求作
证明:
∵点 、
在
上.
∴ ()(填推理依据).
∵
∴ .
∴

a.2013-2020年北京市空气质量指数为优良级别天数变化
b. 收集了2021年3月北京市16个城区的PM2.5的浓度均值(单位:微克/立方米),79 79 80 81 83 79 83 83 81 83 84 84 84 84 86 84并整理如下表:
| PM2.5的浓度 | 79 | 80 | 81 | 83 | 84 | 86 |
| 区的个数 | m | 1 | 2 | n | 5 | 1 |
C.2021年3月北京市每日的PM2.5的浓度(单位:微克/立方米)统计情况如下: