江苏省宿迁市2021年中考数学仿真模拟试卷

更新时间：2021-05-31 浏览次数：189 类型：中考模拟

一、选择题

1. (2018·温州模拟) ﹣5的绝对值是（）

A . 5 B . 1 C . 0 D . ﹣5

答案解析收藏纠错 + 选题
2. (2012·本溪) 下列计算正确的是（　　）

A . a²+a³=a⁵ B . （a²）³=a⁵ C . 2a•3a=6a D . （2a³b）²=4a⁶b²

答案解析收藏纠错 + 选题
3. (2021九下·渝中期中) 下列说法正确的是（）

A . 端午节为保证大家能吃上放心的棕子，质监部门对重庆市市场上的棕子实行全面调查 B . 一组数据﹣1，2，5，7，7，的众数是7，中位数是7 C . 海底捞月是必然事件 D . 甲、乙两名同学各跳远10次，若他们跳远成绩的平均数相同，甲同学跳远成绩的方差为1.2，乙同学跳远成绩的方差为1.6，则甲同学跳远发挥比乙同学稳定

答案解析收藏纠错 + 选题
4. (2020八上·临朐期末) 如图，直线 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的度数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. (2019·广西模拟) 若a>b，则下列不等式成立的是（）

A . a-3<b-3 B . -2a>-2b C . < D . a>b-1

答案解析收藏纠错 + 选题
6. (2015九上·阿拉善左旗期末) 把抛物线y=x²向右平移2个单位，向下平移5个单位得到的抛物线是（）

A . y=x²+3 B . y=x²+7 C . y=（x+2）²﹣5 D . y=（x﹣2）²﹣5

答案解析收藏纠错 + 选题
7. (2023九上·诸暨月考) 从长度分别为2，4，6，8的四条线段中任选三条作边，能构成三角形的概率为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2020九上·郑州月考) 如图，已知正方形ABCD的边长为4，点M和N分别从B、C同时出发，以相同的速度沿BC、CD向终点C、D运动，连接AM、BN，交于点P，连接PC，则PC长的最小值为（）

A . 2 $\text{[math]}$ －2 B . 2 C . 3 $\text{[math]}$ －1 D . 2 $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

9. (2020·铜仁) 因式分解： $\text{[math]}$ .

答案解析收藏纠错 + 选题
10. (2024八下·富锦期末) 若式子 $\text{[math]}$ 在实数范围内有意义，则x的取值范围是．

答案解析收藏纠错 + 选题
11. (2020·萧山模拟) 青盐铁路（青岛一盐城），是我国“八纵八横”高速铁路网中第一纵“沿海通道”的一部分，全长428.752千米.数据428.752千米用科学记数法表示为米.

答案解析收藏纠错 + 选题
12. (2020九上·哈尔滨月考) 不等式组 $\text{[math]}$ 的解集是．

答案解析收藏纠错 + 选题
13. (2019九上·建华期中) 扇形的圆心角为 $\text{[math]}$ ，半径为 $\text{[math]}$ ．若将此扇形围成一个圆锥的侧面（不计接缝），则圆锥的底面积为 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
14. (2020·北京模拟) 已知函数满足下列两个条件：①当 $\text{[math]}$ 时， $\text{[math]}$ 随 $\text{[math]}$ 的增大而减小；②它的图象经过坐标原点，请写出一个符合上述条件的函数的表达式．

答案解析收藏纠错 + 选题
15. (2019九上·龙华期末) 如图，以矩形ABCD的对角线AC为一边向左下方作正方形ACEF，延长AB交EF于点G，若AB=3，BC=4，则EG的长为.

答案解析收藏纠错 + 选题
16. (2024七下·德阳月考) 已知a+b=3，a²+b²=5，则ab的值是

答案解析收藏纠错 + 选题
17. (2020·定远模拟) 如图，在平面直角坐标系xOy中，点B在y轴上，AB=AO，反比例函数y= $\text{[math]}$ 的图象经过点A，若△ABO的面积为2，则k的值为．

答案解析收藏纠错 + 选题
18. (2020九上·上思月考) 如图1，一个扇形纸片的圆心角为90°，半径为6．如图2，将这张扇形纸片折叠，使点A与点O恰好重合，折痕为CD，图中阴影为重合部分，则阴影部分的面积为．(结果保留π和根号的形式)

答案解析收藏纠错 + 选题

三、解答题

19. (2017·南宁模拟) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
20. (2020九下·哈尔滨月考) 先化简，再求代数式 $\text{[math]}$ 的值，其中 $\text{[math]}$ ．

答案解析收藏纠错 + 选题
21. (2017·商丘模拟) 某校260名学生参加植树活动，要求每人植4﹣7棵，活动结束后随机抽查了20名学生每人的植树量，并分为四种类型，A：4棵；B：5棵；C：6棵；D：7棵，将各类的人数绘制成扇形图（如图（1））和条形图（如图（2）），经确认扇形图是正确的，而条形图尚有一处错误．
回答下列问题：
1. （1）写出条形图中存在的错误，并说明理由；
2. （2）写出这20名学生每人植树量的众数、中位数；
3. （3）在求这20名学生每人植树量的平均数时，小宇是这样分析的：
  第一步：求平均数的公式是 $\text{[math]}$ = $\text{[math]}$ ；
  第二步：在该问题中，n=4，x₁=4，x₂=5，x₃=6，x₄=7；
  第三步： $\text{[math]}$ = $\text{[math]}$ =5.5（份）
  ①小宇的分析是从哪一步开始出现错误的？
  ②请你帮他计算出正确的平均数，并估计这260名学生共植树多少棵．
答案解析收藏纠错 + 选题
22. (2021八下·新宾期中) 如图，正方形ABCD的对角线AC、BD相交于点O，E、F分别在OB、OC上，OE＝OF.求证：AE＝BF.

答案解析收藏纠错 + 选题
23. (2015九上·应城期末) 在一个暗箱中装有红、黄、白三种颜色的乒乓球（除颜色外其余均相同），其中白球、黄球各1个，且从中随机摸出一个球是白球的概率是 $\text{[math]}$ ．
1. （1）求暗箱中红球的个数；
2. （2）先从暗箱中随机摸出一个球，记下颜色放回，再从暗箱中随机摸出一个球，求两次摸到的球颜色不同的概率．
答案解析收藏纠错 + 选题
24. 如图，河的两岸MN与PQ相互平行，点A，B是PQ上的两点，C是MN上的点，某人在点A处测得∠CAQ＝30°，再沿AQ方向前进20米到达点B，某人在点A处测得∠CAQ＝30°，再沿AQ方向前进20米到达点B，测得∠CBQ＝60°，求这条河的宽是多少米？（结果精确到0.1米，参考数据 $\text{[math]}$ ≈1.414， $\text{[math]}$ ≈1.732）

答案解析收藏纠错 + 选题
25. (2021九下·苏州开学考) 如图， $\text{[math]}$ ，以 $\text{[math]}$ 为直径的 $\text{[math]}$ 交 $\text{[math]}$ 于点D，点E为弧 $\text{[math]}$ 的中点，连结 $\text{[math]}$ 交 $\text{[math]}$ 于点F，且 $\text{[math]}$ .
1. （1）判断直线 $\text{[math]}$ 与 $\text{[math]}$ 的位置关系，并说明理由；
2. （2）若 $\text{[math]}$ 的半径为2， $\text{[math]}$ ，求 $\text{[math]}$ 的长.
答案解析收藏纠错 + 选题
26. (2016·十堰模拟) 大学生小张利用暑假50天在一超市勤工俭学，被安排销售一款成本为40元/件的新型商品，此类新型商品在第x天的销售量p件与销售的天数x的关系如下表：
x（天）
1
2
3
…
50
p（件）
118
116
114
…
20
销售单价q（元/件）与x满足：当1≤x＜25时q=x+60；当25≤x≤50时q=40+ $\text{[math]}$ ．
1. （1）请分析表格中销售量p与x的关系，求出销售量p与x的函数关系．
2. （2）求该超市销售该新商品第x天获得的利润y元关于x的函数关系式．
3. （3）这50天中，该超市第几天获得利润最大？最大利润为多少？
答案解析收藏纠错 + 选题
27. (2020·桂阳模拟) 如图
1. （1）阅读理解：如图①，在四边形ABCD中，AB∥DC，E是BC的中点，若AE是∠BAD的平分线，试判断AB，AD，DC之间的等量关系．
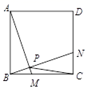
  解决此问题可以用如下方法：延长AE交DC的延长线于点F，易证△AEB≌△FEC，得到AB=FC，从而把AB，AD，DC转化在一个三角形中即可判断．
  
  AB、AD、DC之间的等量关系为；
2. （2）问题探究：如图②，在四边形ABCD中，AB∥DC，AF与DC的延长线交于点F，E是BC的中点，若AE是∠BAF的平分线，试探究AB，AF，CF之间的等量关系，并证明你的结论．
3. （3）问题解决：如图③，AB∥CF，AE与BC交于点E，BE：EC=2：3，点D在线段AE上，且∠EDF=∠BAE，试判断AB、DF、CF之间的数量关系，并证明你的结论．
答案解析收藏纠错 + 选题
28. (2021九上·平罗期末) 如图，抛物线 $\text{[math]}$ 经过 $\text{[math]}$ ， $\text{[math]}$ 两点，且与y轴交于点C，点D是抛物线的顶点，抛物线的对称轴 $\text{[math]}$ 交x轴于点E，连接 $\text{[math]}$ .
1. （1）求经过 $\text{[math]}$ 三点的抛物线的函数表达式；
2. （2）点Q在该抛物线的对称轴上，若 $\text{[math]}$ 是以 $\text{[math]}$ 为直角边的直角三角形，求点Q的坐标；
3. （3）若P为 $\text{[math]}$ 的中点，过点P作 $\text{[math]}$ 轴于点F，G为抛物线上一动点，M为x轴上一动点，N为直线 $\text{[math]}$ 上一动点，当以F、M、N、G为顶点的四边形是正方形时，请求出点M的坐标.
答案解析收藏纠错 + 选题