![]()
如图,图1是由5个完全相同的正方体搭成的几何体,现将标有E的正方体平移至图2所示的位置,下列说法中正确的是( )
①左、右两个几何体的主视图相同
②左、右两个几何体的俯视图相同
③左、右两个几何体的左视图相同.




|
编号 |
教学方式 |
最喜欢的频数 |
频率 |
|
1 |
教师讲,学生听 |
20 |
0.10 |
|
2 |
教师提出问题,学生探索思考 |
0.5 |
|
|
3 |
学生自行阅读教材,独立思考 |
30 |
|
|
4 |
分组讨论,解决问题 |
0.25 |

到个位,参考数据: )
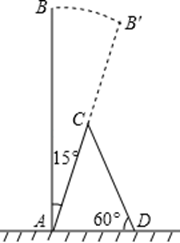

①求 关于
的函数解析式,并写出自变量
的取值范围;
②当 时,直接写出
的面积.