B . 
C . 
D . 
B . 
C . 
D . 
| 摄氏（单位℃） | … | 0 | 1 | 2 | 3 | 4 | 5 | 6 | … |
| 华氏（单位°F） | … | 32 | 33.8 | 35.6 | 37.4 | 39.2 | 41 | 42.8 | … |
那么当华氏度与摄氏度对应相等时的温度值是（ ）
|
1班 |
65 |
70 |
70 |
70 |
75 |
82 |
|
2班 |
55 |
70 |
70 |
75 |
80 |
82 |
请问
，
（填“＞”“＝”或“＜”）
已知：∠AOB
求作：∠ADC ， 使∠ADC＝2∠AOB
作法：如图，
①在射线OB上任取一点C；
②作线段OC的垂直平分线，交OA于点D ， 交OB于点E ， 连接DC ．
所以∠ADC即为所求的角
根据小明设计的尺规作图过程，
证明：∵DE是线段OC的垂直平分线，
∴OD＝ ▲ （ ▲ ）．
∴∠AOB＝ ▲ （ ▲ ）．
∵∠ADC＝∠AOB＋∠DCO ，
∴∠ADC＝2∠AOB ．
a ． 甲、乙两校40名学生成绩的频数分布统计表如下：
|
成绩x 学校 |
50≤x＜60 |
60≤x＜70 |
70≤x＜80 |
80≤x＜90 |
90≤x≤100 |
|
甲 |
4 |
15 |
9 |
10 |
2 |
|
乙 |
6 |
3 |
15 |
14 |
2 |
（说明：成绩80分及以上为优秀，70~79分为良好，60~69分为合格，60分以下为不合格）
b ． 甲校成绩在70≤x＜80这一组的是：70，70，71，72，73，74，76，77，79
c ． 甲、乙两校成绩的平均分、中位数、众数如下：
|
学校 |
平均分 |
中位数 |
众数 |
|
甲 |
74.2 |
n |
85 |
|
乙 |
73.5 |
76 |
84 |
根据以上信息，回答下列问题：
①当a＝2时，画出抛物线的图象，根据图象直接写出m－n的最小值；
②若存在实数t ， 使得m－n＝2，直接写出a的取值范围
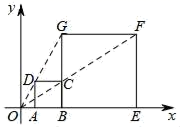
已知点 ．
②若d（线段CD ， 直线AB）＝1，直接写出m的值；
