| 每周用的口罩数量 | 20 | 21 | 23 | 30 |
| 总数 | 3 | 4 | 2 | 1 |
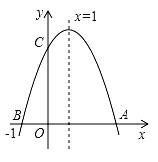
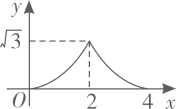 B .
B . 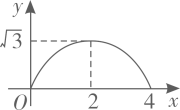 C .
C . 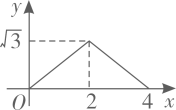 D .
D . 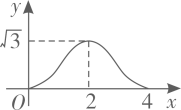



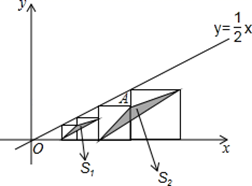

根据统计图提供的信息,解答下列问题:

(结果精确到1米;参考数据: ,
,
)
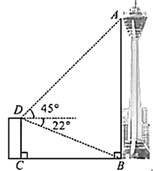


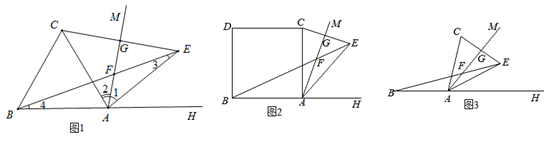
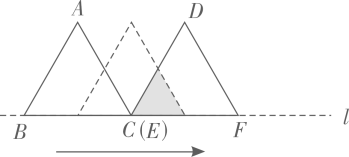
②求证:BF=AF+2FG .
完成下列问题:
①∠FEG= ▲ ;
②线段BF、AF、FG之间存在怎样的数量关系?说明理由.