福建省泉州市南安市2020-2021学年八年级下学期数学期末...

更新时间：2021-08-19 浏览次数：145 类型：期末考试

一、单选题

1. 要使分式 $\text{[math]}$ 有意义， $\text{[math]}$ 必须满足的条件是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. 在平面直角坐标系中，点 $\text{[math]}$ 位于（）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
3. 若一次函数 $\text{[math]}$ 的图象经过点 $\text{[math]}$ ，则 $\text{[math]}$ 的值是（）

A . -1 B . 1 C . 5 D . 7

答案解析收藏纠错 + 选题
4. 2020年6月23日9时43分，我国成功发射了北斗系统第55颗导航卫星，其授时精度为世界之最，不超过0.0000000099秒.数据“0.0000000099”用科学记数法表示为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
5. 某校足球队有16名队员，队员的年龄情况统计如下：

年龄 $\text{[math]}$ 岁

13

14

15

16

人数

3

5

6

2

则这16名队员年龄的众数是（）

A . 5 B . 6 C . 14 D . 15

答案解析收藏纠错 + 选题
6. (2021八下·兖州期末) 如图，在四边形ABCD中，对角线AC和BD相交于点O ，下列条件不能判断四边形ABCD是平行四边形的是（）

A . $\text{[math]}$ ， $\text{[math]}$ B . $\text{[math]}$ ， $\text{[math]}$ C . $\text{[math]}$ ， $\text{[math]}$ D . $\text{[math]}$ ， $\text{[math]}$

答案解析收藏纠错 + 选题
7. 一组数据的方差可以用式子 $\text{[math]}$ 表示，则式子中的数40所表示的意义是（）

A . 这组数据的个数 B . 这组数据的平均数 C . 这组数据的众数 D . 这组数据的中位数

答案解析收藏纠错 + 选题
8. 甲，乙两个工程队，甲队修路 $\text{[math]}$ 米与乙队修路 $\text{[math]}$ 米所用的时间相等，乙队每天比甲队多修 $\text{[math]}$ 米.若可列方程 $\text{[math]}$ 表示题中的等量关系，则方程中 $\text{[math]}$ 表示（）

A . 甲队每天修路的长度 B . 乙队每天修路的长度 C . 甲队修路 $\text{[math]}$ 米所用天数 D . 乙队修路 $\text{[math]}$ 米所用天数

答案解析收藏纠错 + 选题
9. 如图，在矩形ABCD中，AB=4，AD=6，点P在AD上，点Q在BC上，且AP = CQ，连接CP，QD，则PC + QD的最小值为（）

A . 8 B . 10 C . 12 D . 20

答案解析收藏纠错 + 选题
10. 如图，在正方形 $\text{[math]}$ 外取一点 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .过点 $\text{[math]}$ 作 $\text{[math]}$ 的垂线交 $\text{[math]}$ 于点 $\text{[math]}$ .若 $\text{[math]}$ ， $\text{[math]}$ ，下列结论：① $\text{[math]}$ ≌ $\text{[math]}$ ； ②点 $\text{[math]}$ 到直线 $\text{[math]}$ 的距离为 $\text{[math]}$ ；③ $\text{[math]}$ ； ④ $\text{[math]}$ .其中正确结论的序号是（）

A . ①③④ B . ①②③ C . ②③④ D . ①②④

答案解析收藏纠错 + 选题

二、填空题

11. 计算： $\text{[math]}$ ＝

答案解析收藏纠错 + 选题
12. 若一次函数 $\text{[math]}$ 的图象经过第一、二、四象限，则b0（填“＞”或“＜”）.

答案解析收藏纠错 + 选题
13. 甲、乙两名同学参加“古诗词大赛”活动，五次比赛成绩的平均分都是85分，若两人比赛成绩的方差分别为 $\text{[math]}$ 和 $\text{[math]}$ ，则成绩比较稳定的是（填甲或乙）.

答案解析收藏纠错 + 选题
14. (2019八下·汉阳期中) 如图，▱ABCD中，AC、BD相交于点O，若AD=6，AC+BD=16，则△BOC的周长为.

答案解析收藏纠错 + 选题
15. 如图，在 ▱ ABCD中，尺规作图：以点A为圆心，AB的长为半径画弧交AD于点F，分别以点B，F为圆心，以大于BF的长为半径画弧交于点P，作射线AP交BC与点E，若BF = 12，AB = 10，则AE的长为.

答案解析收藏纠错 + 选题
16. 如图，已知在平面直角坐标系 $\text{[math]}$ 中， $\text{[math]}$ 的直角顶点 $\text{[math]}$ 在 $\text{[math]}$ 轴的正半轴上，点 $\text{[math]}$ 在第一象限，反比例函数 $\text{[math]}$ 的图象经过 $\text{[math]}$ 的中点 $\text{[math]}$ .交 $\text{[math]}$ 于点 $\text{[math]}$ ，连接 $\text{[math]}$ .若 $\text{[math]}$ 的面积是3，则四边形 $\text{[math]}$ 的面积是.

答案解析收藏纠错 + 选题

三、解答题

17. 计算： $\text{[math]}$

答案解析收藏纠错 + 选题
18. 先化简，再求值：(x + $\text{[math]}$ )÷(x+1)，其中x=3.

答案解析收藏纠错 + 选题
19. 如图，四边形ABCD中，AD∥BC ，AC、BD相交于点O，O是AC的中点.
求证：四边形ABCD是平行四边形.

答案解析收藏纠错 + 选题
20. 如图，直线 $\text{[math]}$ （ $\text{[math]}$ 为常数， $\text{[math]}$ 与双曲线 $\text{[math]}$ 交于 $\text{[math]}$ ， $\text{[math]}$ 两点，与 $\text{[math]}$ 轴、 $\text{[math]}$ 轴分别交于 $\text{[math]}$ ， $\text{[math]}$ 两点，点 $\text{[math]}$ 的坐标为 $\text{[math]}$ ，点 $\text{[math]}$ 的坐标为 $\text{[math]}$ .
1. （1）求直线的解析式.
2. （2）结合图象直接写出当 $\text{[math]}$ 时， $\text{[math]}$ 的取值范围.
答案解析收藏纠错 + 选题
21. 如图，在□ $\text{[math]}$ 中， $\text{[math]}$ .
1. （1）尺规作图：在 $\text{[math]}$ 边上求作点 $\text{[math]}$ ，使得 $\text{[math]}$ （保留作图痕迹，不写作法）
2. （2）若 $\text{[math]}$ ， $\text{[math]}$ ，求□ $\text{[math]}$ 的面积.
答案解析收藏纠错 + 选题

22. 随着生活节奏的加快以及智能手机的普及，外卖点餐逐渐成为越来越多用户的餐饮消费习惯.由此催生了一批外卖点餐平台，已知某外卖平台的送餐费用与送餐距离有关（该平台只给5千米范围内配送），为调查送餐员的送餐收入，现从该平台随机抽取80名点外卖的用户进行统计，按送餐距离分类统计结果如下表：

送餐距离x（千米）	0＜x ≤1	1＜x ≤2	2＜x ≤3	3＜x ≤4	4＜x ≤5
数量（份）	12	20	24	16	8

（1）设这80名点外卖的用户送餐距离的中位数为m（千米），则m的取值范围是（）

A . 1＜m ≤ 2 B . 2＜m ≤ 3 C . 3＜m ≤ 4 D . 4＜m ≤ 5
（2）以这80名点外卖用户的送餐距离为研究对象，同一组数据取该小组数据的中间值（例如小组（1＜x ≤ 2）的中间值是1.5），计算这80名点餐用户的平均送餐距离；
（3）若该外卖平台给送餐员的送餐费用与送餐距离有关，不超过2千米时，每份3元；超过2千米但不超4千米时，每份5元；超过4千米时，每份9元.以给这80名用户所需送餐费用的平均数为依据，若送餐员一天的目标收入不低于200元，试估计一天至少要送多少份外卖？

答案解析收藏纠错 + 选题

23. 某鞋厂准备生产A，B两种品牌运动鞋共100万双，已知生产每双A种品牌和B种品牌运动鞋共需成本215元，且每双B种品牌运动鞋成本比A种高15元.
1. （1）求A，B两种品牌运动鞋每双的成本分别是多少元；
2. （2） “百年大计，教育为本”，该鞋厂主动扛起支持地方教育发展的使命，每售出1双A种品牌运动鞋就捐出a元来支持地方政府进行助学、奖学.根据市场供需情况，计划生产A种品牌运动鞋至少60万双，B种品牌运动鞋至少20万双.已知A，B两种品牌运动鞋每双售价分别为130元和140元，该鞋厂将如何安排生产才能获得最大利润，最大利润是多少万元？（注：利润＝（销售收入）－（成本）－（捐款））
答案解析收藏纠错 + 选题
24. 在平面直角坐标系中，矩形 $\text{[math]}$ 的顶点 $\text{[math]}$ ， $\text{[math]}$ 分别在 $\text{[math]}$ 轴、 $\text{[math]}$ 轴上，将矩形 $\text{[math]}$ 绕点 $\text{[math]}$ 顺时针旋转角α得到矩形 $\text{[math]}$ ，点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 的对应点分别为 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ .
1. （1）如图1，当 $\text{[math]}$ 过点C时，且 $\text{[math]}$ 的坐标为 $\text{[math]}$ .求 $\text{[math]}$ 的长；
2. （2）如图2，当点 $\text{[math]}$ 落在AC上时，连结 $\text{[math]}$ 、 $\text{[math]}$ .
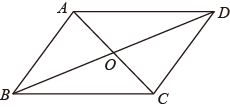
  ① 四边形 $\text{[math]}$ 是何特殊的四边形？请说明理由；
  
  ② 证明点 $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 三点共线.
答案解析收藏纠错 + 选题
25. 如图1，直线 $\text{[math]}$ 分别交 $\text{[math]}$ 轴、 $\text{[math]}$ 轴于 $\text{[math]}$ ， $\text{[math]}$ 两点.
1. （1）直接写出 $\text{[math]}$ 、 $\text{[math]}$ 两点的坐标；
2. （2）如图2，已知直线 $\text{[math]}$ ，无论k取何值，它都经过第一象限内的一个定点 $\text{[math]}$ ，分别连结 $\text{[math]}$ 、 $\text{[math]}$ ，其中 $\text{[math]}$ 交 $\text{[math]}$ 轴于 $\text{[math]}$ 点.
  ① 求 $\text{[math]}$ 的面积；
  
  ② 连接 $\text{[math]}$ ，在直线 $\text{[math]}$ 上是否存在着点 $\text{[math]}$ ，使得 $\text{[math]}$ ？若存在，请直接写出 $\text{[math]}$ 点的坐标（不写求解过程）；若不存在，请说明理由.
答案解析收藏纠错 + 选题