北师版数学九年级上册同步训练《3.2 用频率估计概率》

更新时间：2021-09-15 浏览次数：111 类型：同步测试

一、单选题

1. (2021九上·宁波期中) 育种小组对某品种小麦发芽情况进行测试，在测试基本情况相同的条件下，得到如下数据：

抽查小麦粒数	100	500	1000	2000	3000	4000
发芽粒数	95	486	968	1940	2907	$\text{[math]}$

则a的值最有可能是（）

A . 3680 B . 3720 C . 3880 D . 3960

答案解析收藏纠错 + 选题

2. (2021九上·茂名月考) 在一个不透明的袋子里装有红球，黄球共60个，这些球除颜色外其他都相同.小明通过多次试验发现，摸出红球的频率稳定在0.25左右，则袋子中红球的个数最有可能是（）

A . 9 B . 15 C . 18 D . 24

答案解析收藏纠错 + 选题
3. (2021九上·越城期末) 在一个不透明的袋子里装有5个红球和若干个白球，它们除颜色外其余完全相同，通过多次摸球试验后发现，摸到红球的频率稳定在 $\text{[math]}$ 附近，则估计袋中的白球大约有（）

A . 25 B . 20 C . 15 D . 10

答案解析收藏纠错 + 选题
4. (2024九下·新会月考) 为了解某地区九年级男生的身高情况，随机抽取了该地区100名九年级男生，他们的身高x(cm)统计如下:

组别（cm)

x<160

160≤x<170

170≤x<180

x≥180

人数

5

38

42

15

根据以上结果，抽查该地区一名九年级男生，估计他的身高不低于180cm的概率是（）

A . 0.85 B . 0.57 C . 0.42 D . 0.15

答案解析收藏纠错 + 选题
5. (2022·彭山模拟) 为了估计某地区梅花鹿的数量，先捕捉20只梅花鹿做上标记，然后放走，待有标记的梅花鹿完全混合于鹿群后，第二次捕捉100只梅花鹿，发现其中5只有标记．估计这个地区的梅花鹿的数量约有（）只．

A . 200 B . 300 C . 400 D . 500

答案解析收藏纠错 + 选题
6. (2021·柯桥模拟) 如图，已知不透明的袋中装有红色、黄色、蓝色的乒乓球共120个，某学习小组做“用频率估计概率”的摸球实验（从中随机摸出一个球，记下颜色后放回），统计了“摸出球为红色”出现的频率，绘制了如图折线统计图，那么估计袋中红色球的数目为（）

A . 20 B . 30 C . 40 D . 60

答案解析收藏纠错 + 选题
7. (2024九上·沈丘期末) 下列说法正确的是（）

A . 某彩票的中奖概率是5%，那么买100张彩票一定有5张中奖 B . 某次试验投掷次数是500，计算机记录“钉尖向上”的次数是308，则该次试验“钉尖向上”的频率是0.616 C . 当试验次数很大时，概率稳定在频率附近 D . 试验得到的频率与概率不可能相等

答案解析收藏纠错 + 选题
8. (2021九上·陈仓期中) 某班学生做“用频率估计概率”的实验时，给出的某一结果出现如图所示的统计图，则符合这一结果的实验可能是（　　）

A . 抛一枚硬币，出现正面朝上 B . 从标有1，2，3，4，5，6的六张卡片中任抽一张，出现偶数 C . 从一个装有6个红球和3个黑球的袋子中任取一球，取到的是黑球 D . 先后两次掷一枚质地均匀的正六面体骰子，两次向上的点数之和是7

答案解析收藏纠错 + 选题
9. (2023九上·坪山月考) 一个密闭不透明的盒子里有若干个白球，在不许将球倒出来数的情况下，为了估计白球数，小刚向其中放入了8个黑球，搅匀后从中随意摸出一个球记下颜色，再把它放回盒中，不断重复这一过程，共摸球400次，其中80次摸到黑球，你估计盒中大约有白球（）

A . 32个 B . 36个 C . 40个 D . 42个

答案解析收藏纠错 + 选题
10. (2021九上·贵阳期末) 小明将贵州健康码打印在面积为 $\text{[math]}$ 的正方形纸上，如图所示为了估计图中健康码部分的面积，在纸内随机掷点，经过大量重复试验，发现点落入健康码部分的频率稳定在0.6左右，据此可以估计健康码部分的面积约为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题

二、填空题

11. (2021·太原模拟) 在同样条件下，对某种小麦种子进行发芽试验，统计如下表：

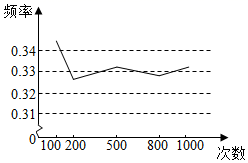
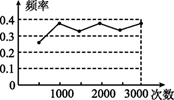
试验种子粒数	50	100	200	500	1000	2000	3000
发芽种子粒数	45	92	188	476	951	1900	2850

据此估计该小麦种子发芽的概率为（精确到0.01）．

答案解析收藏纠错 + 选题

12. (2024九下·北京市模拟) 在一个不透明的袋子里装有红球和白球共30个，这些球除颜色外都相同，小明通过多次试验发现，摸出白球的频率稳定在0.3左右，则袋子里白球可能是个．

答案解析收藏纠错 + 选题

13. (2021·花溪模拟) 把一枚木质中国象棋子“兵”从一定高度落下，落地后“兵”字面可能朝上，也可能朝下.为了估计“兵”字面朝上的概率，某实验小组做了棋子下掷实验数据如下表：

实验次数 $\text{[math]}$	20	60	100	120	140	160	500	1000	2000	5000
“兵”字面朝上次数 $\text{[math]}$	14	38	52	66	78	88	280	550	1100	2750
“兵”字面朝上频率 $\text{[math]}$	0.7	0.63	0.52	0.55	0.56	0.55	0.56	0.55	0.55	0.55

下面有三个推断：①投掷1000次时，“兵”字面朝上的次数是550，所以“兵”字面朝上的概率是0.55；②随着实验次数的增加，“兵”字面朝上的频率总在0.55附近，显示出一定的稳定性，可以估计“兵”字面朝上的概率是0.55；③当实验次数为200次时，“兵”字面朝上的频率一定是0.55.其中合理的是.（填序号①、②、③）

答案解析收藏纠错 + 选题

14. (2021九下·北京月考) 某小组做“用频率估计概率”的试验时，统计了某一事件发生的频率，绘制了如图所示的折线图．

该事件最有可能是（填写一个你认为正确的序号）．

①掷一个质地均匀的正六面体骰子，向上一面的点数是2；

②掷一枚硬币，正面朝上；

③暗箱中有1个红球和2个黄球，这些球除了颜色外无其他差别，从中任取一球是红球．

答案解析收藏纠错 + 选题
15. (2024九下·兴庆模拟) 在一个不透明的暗箱中装有红、黄、蓝三种除颜色外完全相同的小球，其中红球5个，黄球7个，蓝球a个.若每次将球充分搅匀后，随机摸出一个小球记下颜色后，放回盒子里，经过大量的重复试验后发现，摸到红球的频率稳定在25%左右，则a的值约为.

答案解析收藏纠错 + 选题
16. (2020九上·朝阳期末) 不透明的盒子中装有红、黄色的小球共20个，除颜色外无其他差别，随机摸出一个小球，记录颜色后放回并摇匀，再随机摸出一个．下图显示了某数学小组开展上述摸球活动的某次实验的结果．

下面有四个推断：

①当摸球次数是300时，记录“摸到红球”的次数是99，所以“摸到红球”的概率是0.33；

②随着试验次数的增加，“摸到红球”的频率总在0.35附近摆动，显示出一定的稳定性，可以估计“摸到红球”的概率是0.35；

③可以根据本次实验结果，计算出盒子中约有红球7个；

④若再次开展上述摸球活动，则当摸球次数为500时，“摸到红球”的频率一定是0.40

所有合理推断的序号是．

答案解析收藏纠错 + 选题

三、解答题

17. (2021九上·富县期末) 4件同型号的产品中，有1件不合格品和3件合格品.在这4件产品中加入 $\text{[math]}$ 件合格品后，进行如下试验：随机抽取1件进行检测，然后放回，多次重复这个试验，通过大量重复试验后发现，抽到合格品的频率稳定在0.95，由此可以推算出 $\text{[math]}$ 的值大约是多少？

答案解析收藏纠错 + 选题
18. 某人承包了一池塘养鱼，他想估计一下收入情况.于是让他上初三的儿子帮忙.他儿子先让他从鱼塘里随意打捞上了60条鱼，把每条鱼都作上标记，放回鱼塘；过了2天，他让他父亲从鱼塘内打捞上了50条鱼，结果里面有2条带标记的.假设当时这种鱼的市面价为2.8元/斤，平均每条鱼估计2.3斤，你能帮助他估计一下今年的收入情况吗?

答案解析收藏纠错 + 选题
19. 某封闭的纸箱中有红色、黄色的玻璃球若干，为了估计出纸箱中红色、黄色球的数目，小亮向纸箱中放入25个白球，通过多次摸球实验后，发现摸到白球的频率为25％，摸到黄球的频率为40％，试估计出原纸箱中红球、黄球的数目．

答案解析收藏纠错 + 选题
20. 对某厂生产的直径为4cm的乒乓球进行产品质量检查，结果如下：
1. （1）计算各次检查中“优等品”的频率，填入表中；
  抽取球数n 50 100 500 1000 5000
  优等品数m 45 92 455 890 4500
  优等品频率 $\text{[math]}$
2. （2）该厂生产乒乓球优等品的概率约为多少?
答案解析收藏纠错 + 选题
21. (2022九上·桐庐月考) 目前我市“校园手机”现象越来越受到社会关注，针对这种现象，我市某中学九年级数学兴趣小组的同学随机调查了学校若干名家长对“中学生带手机”现象的看法，统计整理并制作了如下的统计图：
1. （1）这次调查的家长总数为人．家长表示“不赞同”的人数为人；
2. （2）请在图①中把条形统计图补充完整；
3. （3）从这次接受调查的家长中随机抽查一个，恰好是“赞同”的家长的概率是；
4. （4）求图②中表示家长“无所谓”的扇形圆心角的度数．
答案解析收藏纠错 + 选题

22. (2022九上·南海月考) 一只不透明袋子中装有1个白球和若干个红球，这些球除颜色外都相同，某课外学习小组做摸球试验：将球搅匀后从中任意摸出1个球，记下颜色后放回、搅匀，不断重复这个过程，获得数据如下：

摸球的次数	200	300	400	1000	1600	2000
摸到白球的频数	72	93	130	334	532	667
摸到白球的频率	0.3600	0.3100	0.3250	0.3340	0.3325	0.3335

（1）该学习小组发现，随着摸球次数的增多，摸到白球的频率在一个常数附近摆动，请直接写出这个常数（精确到0.01），由此估出红球有几个？
（2）在这次摸球试验中，从袋中随机摸出1个球，记下颜色后放回，再从中随机摸出1个球，利用画树状图或列表的方法表示所有可能出现的结果，并求两次摸到的球恰好1是个白球，1个是红球的概率．

答案解析收藏纠错 + 选题

试卷信息

小学

初中

高中

北师版数学九年级上册同步训练《3.2 用频率估计概率》

副标题：

*注意事项：

北师版数学九年级上册同步训练《3.2 用频率估计概率》

数学考试

试题分析

总体分析

题量分析

难度分析

知识点分析

抽取球数n	50	100	500	1000	5000
优等品数m	45	92	455	890	4500
优等品频率 $\text{[math]}$

组别（cm)	x<160	160≤x<170	170≤x<180	x≥180
人数	5	38	42	15