| 成绩(分) | 90 | 91 | 95 | 96 | 97 | 99 |
| 人数(人) | 2 | 3 | 2 | 4 | 3 | 1 |
则这组数据的中位数和众数分别为( )
 B .
B .  C .
C .  D .
D . 
| 甲 | 乙 | 丙 | 丁 | |
| 平均数 | 11.1 | 11.1 | 10.9 | 10.9 |
| 方差s2/米2 | 1.1 | 1.2 | 1.3 | 1.4 |

| x | 6.17 | 6.18 | 6.19 | 6.20 |
| y=ax2+bx+c | ﹣0.03 | ﹣0.01 | 0.02 | 0.04 |
根据表中数据判断,方程ax2+bx+c=0的一个解x的范围是( )


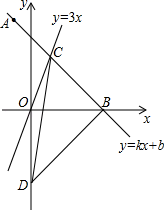
|
分数 人数 年级 |
80 |
85 |
90 |
95 |
100 |
平均数 |
中位数 |
众数 |
方差 |
||
|
七年级 |
2 |
2 |
3 |
2 |
1 |
七年级 |
89 |
|
90 |
39 |
|
|
八年级 |
1 |
2 |
4 |
|
1 |
八年级 |
|
90 |
|
30 |
请根据以上信息,解答下列问题:

②若-3≤x≤0时,二次函数y=x2+mx+n的最小值为-4,求m的值.
