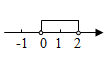
 B .
B . 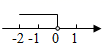 C .
C . 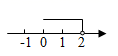 D .
D . 






在平面直角坐标系xOy中有不重合的两点A(x1 , y1)和点B(x2 , y2),小明在学习中发现,若x1=x2 , 则AB∥y轴,且线段AB的长度为|y1﹣y2|;若y1=y2 , 则AB∥x轴,且线段AB的长度为|x1﹣x2|;

①若点A(﹣1,1)、B(2,1),则AB∥x轴,AB的长度为.
②若点C(1,0),且CD∥y轴,且CD=2,则点D的坐标为.
我们规定:平面直角坐标系中任意不重合的两点M(x1 , y1),N(x2 , y2)之间的折线距离为d(M,N)=|x1﹣x2|+|y1﹣y2|;例如:图1中,点M(﹣1,1)与点N(1,﹣2)之间的折线距离为d(M,N)=|﹣1﹣1|+|1﹣(﹣2)|=2+3=5.
解决下列问题:
①如图1,已知E(2,0),若F(﹣1,﹣2),则d(E,F);
②如图2,已知E(2,0),H(1,t),若d(E,H)=3,则t=.
③如图3,已知P(3,3),点Q在x轴上,且三角形OPQ的面积为3,则d(P,Q)=.
