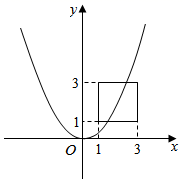广东省中山市2020-2021学年九年级上学期数学期末试卷

更新时间：2021-09-28 浏览次数：161 类型：期末考试

一、单选题

1. (2019八下·丹江口期末) 下列交通标志中，是中心对称图形的是（　　）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2020·通辽) 下列事件中是不可能事件的是（）

A . 守株待兔 B . 瓮中捉鳖 C . 水中捞月 D . 百步穿杨

答案解析收藏纠错 + 选题
3. 一元二次方程 $\text{[math]}$ ﹣16＝0的解是（）

A . x＝4 B . $\text{[math]}$ ＝4， $\text{[math]}$ ＝0 C . $\text{[math]}$ ＝4， $\text{[math]}$ ＝﹣4 D . x＝8

答案解析收藏纠错 + 选题
4. (2016九上·永城期中) 将抛物线y= $\text{[math]}$ x²向左平移一个单位，所得抛物线的解析式为（）

A . y= $\text{[math]}$ x²+1 B . y= $\text{[math]}$ x²﹣1 C . y= $\text{[math]}$ （x+1）² D . y= $\text{[math]}$ （x﹣1）²

答案解析收藏纠错 + 选题
5. (2019·湖州) 已知现有的10瓶饮料中有2瓶已过了保质期，从这10瓶饮料中任取1瓶，恰好取到已过了保质期的饮料的概率是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2018·来宾模拟) 某班同学毕业时，都将自己的照片向全班其他同学各送一张表示留念，全班共送1892张照片，如果全班有x名同学，根据题意，列出方程为（）

A . x（x+1）=1892 B . x（x−1）=1892×2 C . x（x−1）=1892 D . 2x（x+1）=1892

答案解析收藏纠错 + 选题
7. (2020·内江) 如图，点A ， B ， C ， D在⊙O上， $\text{[math]}$ ，点B是 $\text{[math]}$ 的中点，则 $\text{[math]}$ 的度数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2020·苏州) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ，将 $\text{[math]}$ 绕点A按逆时针方向旋转得到 $\text{[math]}$ .若点 $\text{[math]}$ 恰好落在 $\text{[math]}$ 边上，且 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2018九上·武汉期末) 圆的直径是13cm，如果圆心与直线上某一点的距离是6.5cm，那么该直线和圆的位置关系是（）

A . 相离 B . 相切 C . 相交 D . 相交或相切

答案解析收藏纠错 + 选题
10. (2021·建湖模拟) 从地面竖直向上抛出一小球，小球的高度h（单位：m）与小球运动时间t（单位：s）之间的函数关系如图所示.下列结论：①小球抛出3秒时达到最高点；②小球从抛出到落地经过的路程是80m；③小球的高度h＝20时，t＝1s或5s.④小球抛出2秒后的高度是35m.其中正确的有（）

A . ①② B . ②③ C . ①③④ D . ①②③

答案解析收藏纠错 + 选题

二、填空题

11. (2018九上·武昌期中) 已知点A（a，1）与点A′（5，b）是关于原点对称，则a+b =.

答案解析收藏纠错 + 选题
12. 若某扇形花坛的面积为6m² ，半径为3m，则该扇形花坛的弧长为m．

答案解析收藏纠错 + 选题

13. (2020九上·杭州月考) 某林业部门统计某种幼树在一定条件下的移植成活率，结果如下表所示：

移植总数（n）	200	500	800	2000	12000
成活数（m）	187	446	730	1790	10836
成活的频率 $\text{[math]}$	0.935	0.892	0.913	0.895	0.903

根据表中数据，估计这种幼树移植成活率的概率为（精确到0.1）.

答案解析收藏纠错 + 选题

14. 已知正六边形的边长为2，则它的内切圆的半径为．

答案解析收藏纠错 + 选题
15. 如图， $\text{[math]}$ ABC的内切圆与三边分别相切于点D、E、F，若∠B＝50°，则∠EDF＝度．

答案解析收藏纠错 + 选题
16. 如图，正方形四个顶点的坐标依次为(1，1)，(3，1)，(3，3)，(1，3)，若抛物线y＝ax²的图象与正方形的边有公共点，则实数a的取值范围是．

答案解析收藏纠错 + 选题
17. 如图，在△ABC中，AB=10，AC=8，BC=6，以边AB的中点O为圆心，作半圆与AC相切，点P，Q分别是边BC和半圆上的动点，连接PQ，则PQ长的最小值是.

答案解析收藏纠错 + 选题

三、解答题

18. 已知关于x的一元二次方程（a+1）x²+2x+1﹣a²＝0有一个根为﹣1，求a的值．

答案解析收藏纠错 + 选题
19. 在下面的网格图中，每个小正方形的边长均为1， $\text{[math]}$ ABC的三个顶点都是网格线的交点，已知A，B，C的坐标分别为(0，2)，(﹣1，﹣1)，(1，﹣2)，将 $\text{[math]}$ ABC绕着点C顺时针旋转90°得到 $\text{[math]}$ ．在图中画出 $\text{[math]}$ 并写出点 $\text{[math]}$ 、点 $\text{[math]}$ 的坐标．

答案解析收藏纠错 + 选题
20. 如图在⊙O中，OA是半径，OA＝4．
1. （1）用直尺和圆规作OA的垂直平分线BC，BC交OA于点D，交⊙O于点B、C（保留作图痕迹，不要求写作法）；
2. （2）在第（1）问的基础上，求线段BC的长度．
答案解析收藏纠错 + 选题
21. (2020·南京) 甲、乙两人分别从A、B、C这3个景点随机选择2个景点游览.
1. （1）求甲选择的2个景点是A、B的概率.
2. （2）甲、乙两人选择的2个景点恰好相同的概率是.
答案解析收藏纠错 + 选题
22. 若a²+b²＝c² ，则我们把形如ax²+ $\text{[math]}$ cx+b＝0（a≠0）的一元二次方程称为“勾系一元二次方程”．
1. （1）当a＝3，b＝4时，写出相应的“勾系一元二次方程”；
2. （2）求证：关于x的“勾系一元二次方程”ax²+ $\text{[math]}$ cx+b＝0（a≠0）必有实数根．
答案解析收藏纠错 + 选题
23. 如图，利用一面长为34米的墙，用铁栅栏围成一个矩形自行车场地ABCD，在AB和BC边各有一个2米宽的小门（不用铁栅栏）．若所用铁栅栏的长为40米，矩形ABCD的边AD长为x米，AB长为y米，矩形的面积为S平方米，且x＜y．
1. （1）求y与x的函数关系式，并直接写出自变量x的取值范围；
2. （2）求S与x的函数关系式，并求出矩形场地的最大面积．
答案解析收藏纠错 + 选题
24. 如图，⊙O的半径为1，直线CD经过圆心O，交⊙O于C、D两点，直径AB⊥CD，点M是直线CD上异于点C、O、D的一个动点，AM所在的直线交于⊙O于点N，点P是直线CD上另一点，且PM＝PN．
1. （1）当点M在⊙O内部，如图①，试判断PN与⊙O的关系，并写出证明过程；
2. （2）当点M在⊙O外部，如图②，其它条件不变时，（1）的结论是否成立？请说明理由；
3. （3）当点M在⊙O外部，如图③，∠AMO＝30°，求图中阴影部分的面积．
答案解析收藏纠错 + 选题
25. 如图，在平面直角坐标系中，抛物线l₁：y＝x²+bx+c过点C(0，﹣3)，且与抛物线l₂：y＝﹣ $\text{[math]}$ x²﹣ $\text{[math]}$ x+2的一个交点为A，已知点A的横坐标为2．点P、Q分别是抛物线l₁、抛物线l₂上的动点．
1. （1）求抛物线l₁对应的函数表达式；
2. （2）若点P在点Q下方，且PQ∥y轴，求PQ长度的最大值；
3. （3）若以点A、C、P、Q为顶点的四边形为平行四边形，直接写出点P的坐标．
答案解析收藏纠错 + 选题