福建省福州市则徐中学2021-2022学年九年级上学期数学第...

更新时间：2021-11-19 浏览次数：71 类型：月考试卷

一、单选题

1. (2022八下·凤县期中) 下列轴对称图形中，是中心对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2024九下·广州开学考) 已知一元二次方程x²+kx-3=0有一个根为1，则k的值为（）

A . −2 B . 2 C . −4 D . 4

答案解析收藏纠错 + 选题
3. (2021九上·温州月考) 二次函数 $\text{[math]}$ 得顶点坐标是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2024九下·开原模拟) 下列对一元二次方程x²+x﹣3=0根的情况的判断，正确的是（）

A . 有两个不相等实数根 B . 有两个相等实数根 C . 有且只有一个实数根 D . 没有实数根

答案解析收藏纠错 + 选题
5. (2024九上·汉川月考) 已知(﹣3， $\text{[math]}$ )，(﹣2， $\text{[math]}$ )，(1， $\text{[math]}$ )是抛物线 $\text{[math]}$ 上的点，则（）

A . $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ B . $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ C . $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ D . $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$ $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2021九上·福州月考) 如图，△ADE旋转到△CDB，点A与点C是对应点，下列说法错误的是（）

A . AE∥BD B . AD＝DC C . DE平分∠ADB D . AE＝BC

答案解析收藏纠错 + 选题
7. (2024九上·珠海月考) 一元二次方程 $\text{[math]}$ 配方后可化为（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
8. (2021九上·福州月考)
如图是抛物线形拱桥，当拱顶高离水面2m时，水面宽4m．水面下降2.5m，水面宽度增加（　　）

A . 1m B . 2m C . 3m D . 6m

答案解析收藏纠错 + 选题
9. (2021九上·福州月考) 某纪念品原价150元，连续两次降价 $\text{[math]}$ 后，售价为98元，下列方程正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2021九上·福州月考) 已知二次函数 $\text{[math]}$ 的图象如图，则下列结论中正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$ 的符号无法确定

答案解析收藏纠错 + 选题

二、填空题

11. (2021九上·福州月考) 在平面直角坐标系中，点 $\text{[math]}$ 关于原点对称的点的坐标为．

答案解析收藏纠错 + 选题
12. (2023九上·广宁期中) 一元二次方程 $\text{[math]}$ 的根是．

答案解析收藏纠错 + 选题
13. (2024九下·南岗模拟) 如果将抛物线y=x²向上平移3个单位，那么所得新抛物线的表达式是．

答案解析收藏纠错 + 选题
14. (2021九上·福州月考) 抛物线 $\text{[math]}$ 经过点 $\text{[math]}$ 、 $\text{[math]}$ 两点，则关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 的解是.

答案解析收藏纠错 + 选题
15. (2021九上·福州月考) 如图，直线 $\text{[math]}$ 与x轴、y轴分别交于A、B两点，把 $\text{[math]}$ 绕点B逆时针旋转90°后得到 $\text{[math]}$ ，则点 $\text{[math]}$ 的坐标是.

答案解析收藏纠错 + 选题

16. (2021九上·福州月考) 老师给出了二次函数y＝ax²＋bx＋c（a≠0）的部分对应值如表：

x	…	﹣3	﹣2	0	1	3	5	…
y	…	7	0	﹣8	﹣9	﹣5	7	…

下列结论，①抛物线的开口向上；②抛物线的对称轴为直线x＝2；③当﹣2＜x＜4时，y＜0；④x＝3是方程ax²＋bx＋c＋5＝0的一个根；⑤若A（x₁ ， 5），B（x₂ ， 6）是抛物线上两点，则x₁＜x₂ ，其中正确的是（只填写序号）.

答案解析收藏纠错 + 选题

三、解答题

17. (2024九上·鹿寨期末) 解方程： $\text{[math]}$

答案解析收藏纠错 + 选题
18. (2021九上·福州月考) 已知关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ .
1. （1）求证：无论 $\text{[math]}$ 取何值，此方程总有两个不相等的实数根；
2. （2）若方程有两个实数根 $\text{[math]}$ ， $\text{[math]}$ ，且 $\text{[math]}$ ，求 $\text{[math]}$ 的值.
答案解析收藏纠错 + 选题
19. (2022八下·天桥期末) 如图，方格纸中每个小正方形的边长都是1个单位长度，在方格纸中建立如图所示的平面直角坐标系．△ABC的顶点都在格点上．
1. （1）将△ABC 向右平移 6个单位长度得到△A₁B₁C₁ ，请画出△A₁B₁C₁；
2. （2）画出△A₁B₁C₁关于点O的中心对称图形△A₂B₂C₂：
3. （3）若将△ABC 绕某一点旋转可得到△A₂B₂C₂ ，请直接写出旋转中心的坐标.
答案解析收藏纠错 + 选题
20. (2024九上·蛟河期末) 某景区商店销售一种纪念品，每件的进货价为40元．经市场调研，当该纪念品每件的销售价为50元时，每天可销售200件；当每件的销售价每增加1元，每天的销售数量将减少10件．
1. （1）当每件的销售价为52元时，该纪念品每天的销售数量为件；
2. （2）当每件的销售价x为多少时，销售该纪念品每天获得的利润y最大？并求出最大利润．
答案解析收藏纠错 + 选题
21. (2021九上·台安期中) 某幢建筑物从10米高的窗户A用水管向外喷水，喷出的水流呈抛物线状(如图)，若抛物线最高点M离墙1米，离地面 $\text{[math]}$ 米.问：
1. （1）求抛物线的解析式；
2. （2）求水流落地点B离墙的距离
答案解析收藏纠错 + 选题
22. (2021九上·福州月考) 如图，等腰直角 $\text{[math]}$ 中， $\text{[math]}$ ，点D，E在 $\text{[math]}$ 上， $\text{[math]}$ .
1. （1）将 $\text{[math]}$ 绕点C逆时针旋转 $\text{[math]}$ ，点D对应点为点F，画出旋转后的图形，并证明： $\text{[math]}$ ；
2. （2）求证： $\text{[math]}$ .
答案解析收藏纠错 + 选题
23. (2022九上·潜山月考) 已知抛物线 $\text{[math]}$ ．
1. （1）求这条抛物线的对称轴；
2. （2）若该抛物线的顶点在x轴上，求其解析式；
3. （3）设点 $\text{[math]}$ ， $\text{[math]}$ 在抛物线上，若 $\text{[math]}$ ，求m的取值范围．
答案解析收藏纠错 + 选题
24. (2021九上·福州月考) 在平面直角坐标系中，四边形 $\text{[math]}$ 是矩形，点A的坐标为 $\text{[math]}$ ，点B的坐标为 $\text{[math]}$ ，以点A为中心，顺时针旋转矩形 $\text{[math]}$ ，得到矩形 $\text{[math]}$ ，点O，B，C的对应点分别为D，E，F.
1. （1）如图①，当点D落在 $\text{[math]}$ 边上时，求点D的坐标；
2. （2）如图②，当点D落在线段 $\text{[math]}$ 上时，连接 $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 交于点H.
  ①求证： $\text{[math]}$ ；
  
  ②求点H的坐标.
3. （3）点K为矩形 $\text{[math]}$ 对角线的交点，S为 $\text{[math]}$ 得面积，直接写出S的取值范围.
答案解析收藏纠错 + 选题
25. (2021九上·福州月考) 已知二次函数y=ax²+bx+c图象的对称轴为y轴，且过点(1，2)，(2，5).
1. （1）求二次函数的解析式；
2. （2）如图，过点E(O，2)的一次函数图象与二次函数的图象交于A，B两点（A点在B点的左侧），过点A，B分别作AC⊥x轴于点C，BD⊥x轴于点D。
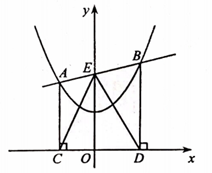
  ①当CD=3时，求该一次函数的解析式；
  
  ②分别用S₁ ， S₂ ， S₃表示△ACE，△ECD，△EDB的面积，问是否存在实数t，使得 $\text{[math]}$ =tS₁S₃ ，都成立？若存在，求出t的值；若不存在，说明理由。
答案解析收藏纠错 + 选题