北京市第四中学2021-2022学年九年级上学期数学开学考试...

更新时间：2021-10-25 浏览次数：152 类型：开学考试

一、单选题

1. (2021九上·北京开学考) 下列二次根式中，是最简二次根式的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
2. (2024八下·北京市期中) 以下列长度的三条线段为边，能组成直角三角形的是（）

A . 1；1；1 B . 2；3；4 C . 1； $\text{[math]}$ ；2 D . $\text{[math]}$ ；3；5

答案解析收藏纠错 + 选题
3. (2023八下·宜州期末) 菱形具有而平行四边形不具有的性质是（　　）

A . 两组对边分别平行 B . 两组对角分别相等 C . 对角线互相平分 D . 对角线互相垂直

答案解析收藏纠错 + 选题
4. (2021九上·北京开学考) 下表是校女子排球队12名队员的年龄分布：

年龄（岁）

13

14

15

16

人数（名）

1

4

5

2

则关于这12名队员的年龄的说法正确的是（）

A . 中位数是14 B . 中位数是14.5 C . 众数是15 D . 众数是5

答案解析收藏纠错 + 选题
5. (2021九上·北京开学考) 用配方法解一元二次方程 $\text{[math]}$ ，配方变形过程正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2021九上·北京开学考) 如图，在 $\text{[math]}$ 中，点D，点E分别是 $\text{[math]}$ 的中点，点F是 $\text{[math]}$ 上一点，且 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A . 1 B . 2 C . 3 D . 4

答案解析收藏纠错 + 选题
7. (2021九上·北京开学考) 若图中反比例函数的表达式均为 $\text{[math]}$ ，则阴影面积为4的有（）

A . 1个 B . 2个 C . 3个 D . 4个

答案解析收藏纠错 + 选题
8. (2021九上·北京开学考) 为规范市场秩序、保障民生工程，监管部门对某一商品的价格持续监控．该商品的价格 $\text{[math]}$ （元/件）随时间t（天）的变化如图所示，设 $\text{[math]}$ （元/件）表示从第1天到第t天该商品的平均价格，则 $\text{[math]}$ 随t变化的图像大致是（）

A . B . C . D .

答案解析收藏纠错 + 选题

二、填空题

9. (2024九上·北京市开学考) 若二次根式 $\text{[math]}$ 在实数范围内有意义，则x的取值范围是．

答案解析收藏纠错 + 选题
10. (2021九上·北京开学考) 如图所示的网格是正方形网格，A，B，C，D是网格线交点，则 $\text{[math]}$ 与 $\text{[math]}$ 的大小关系为： $\text{[math]}$ $\text{[math]}$ （填“＞”，“＝”或“＜”）．

答案解析收藏纠错 + 选题
11. (2021九上·北京开学考) 已知点 $\text{[math]}$ 都在反比例函数 $\text{[math]}$ 的图象上，且 $\text{[math]}$ ，则 $\text{[math]}$ $\text{[math]}$ （填“>”，“=”或“<”）

答案解析收藏纠错 + 选题
12. (2023九上·青铜峡期中) 如果关于 $\text{[math]}$ 的一元二次方程 $\text{[math]}$ 的一个解是 $\text{[math]}$ ，那么代数式 $\text{[math]}$ 的值是．

答案解析收藏纠错 + 选题
13. (2023九上·宝安期中) 如图，在菱形ABCD中，对角线AC与BD相交于点O，AC=8，BD=6，OE⊥BC，垂足为点E，则OE=．

答案解析收藏纠错 + 选题
14. (2021九上·北京开学考) 反比例函数 $\text{[math]}$ （k为整数，且k≠0）在第一象限的图象如图所示，已知图中点A的坐标为（2，1），则k的值是．

答案解析收藏纠错 + 选题
15. (2021九上·北京开学考) 小宇在纸上写了六个两两不等的数 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，并记录下这组数的中位数 $\text{[math]}$ 和方差 $\text{[math]}$ ，然后他将这六个数中大于 $\text{[math]}$ 的三位数分别加1，小于 $\text{[math]}$ 的三个数分别减1，得到了新的一组数，再次记录下新的这组数的中位数 $\text{[math]}$ 和方差 $\text{[math]}$ ，则 $\text{[math]}$ $\text{[math]}$ ， $\text{[math]}$ $\text{[math]}$ ．（两空均填“ $\text{[math]}$ ”“=”或“ $\text{[math]}$ ”）

答案解析收藏纠错 + 选题

16. (2021九上·北京开学考) 2020年9月22日，中国政府在第七十五届联合国大会上提出：“中国将提高国家自主贡献力度，采取更加有力的政策和措施，二氧化碳排放力争于2030年前达到峰值，努力争取2060年前实现碳中和．”所谓碳中和是指企业、团体或个人测算在一定时间内，直接或间接产生的温室气体排放总量，通过植树造林、节能减排等形式，抵消自身产生的二氧化碳排放，实现二氧化碳的“零排放”．某同学设计了一种碳足迹标签帮助大家了解某一产品或服务所产生的碳排放量多少，如图所示．

碳足迹标签是一种碳排放量的标示方式．碳足迹标签的数据标示有其规定，以碳排放量大于20克且不超过40克为例，此范围内的碳足迹数据标示只有20、22、24、…、38、40克等11个偶数；碳足迹数据标示决定于碳排放量与这11个偶数之中的哪一个差距最小，两者对应标示的范例如下表所示．

碳排放量	碳足迹数据标示
20.2克	20克
20.8克	20克
21.0克	20克或22克皆可
23.1克	24克

请根据上述信息，回答下列问题．

（1）若有一个产品的碳足迹数据标示为38克，则它可能的碳排放量最小值为克，最大值为克．
（2）对于（1）中的产品，当其碳排放量减少为原本的90%时，此产品碳足迹数据标示的所有可能为克．

答案解析收藏纠错 + 选题

三、解答题

17. (2021九上·北京开学考) 计算： $\text{[math]}$ ．

答案解析收藏纠错 + 选题
18. (2021九上·北京开学考) 解方程：
1. （1） $\text{[math]}$ ；
2. （2） $\text{[math]}$ ．
答案解析收藏纠错 + 选题
19. (2021九上·北京开学考) 开发商准备以每平方米20000元价格出售某楼盘，为遵循政府有关房地产的调控政策，开发商经过两次下调销售价格后，决定以每平方米16200元的价格销售．
1. （1）求平均每次下调的百分率；
2. （2）房产销售经理向开发商建议：先公布下调5%，再下调15%，这样更有吸引力，请问房产销售经理的方案对购房者是否更优惠？为什么？
答案解析收藏纠错 + 选题
20. (2021九上·北京开学考) 已知：如图，B，D是平行四边形 $\text{[math]}$ 的对角线 $\text{[math]}$ 所在直线上两点，且 $\text{[math]}$ ．
求证：四边形 $\text{[math]}$ 是平行四边形．

答案解析收藏纠错 + 选题
21. (2021九上·北京开学考) 已知关于x的方程 $\text{[math]}$ 。
1. （1）求证：此方程总有实数根；
2. （2）若m为整数，且此方程有两个互不相等的负整数根，求m的值；
答案解析收藏纠错 + 选题
22. (2021九上·北京开学考) 如图，一次函数 $\text{[math]}$ 与反比例函数 $\text{[math]}$ 的图象交于 $\text{[math]}$ 和 $\text{[math]}$ 两点．
1. （1）直接写出 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ；
2. （2）结合图象直接写出关于x的不等式 $\text{[math]}$ 的解集是；
3. （3）点 $\text{[math]}$ 在反比例函数 $\text{[math]}$ 的图象上，连接 $\text{[math]}$ 、 $\text{[math]}$ ，求 $\text{[math]}$ 的面积．
答案解析收藏纠错 + 选题
23. (2023八下·西山期末) 如图，在 $\text{[math]}$ 中，过点 $\text{[math]}$ 作 $\text{[math]}$ 于点 $\text{[math]}$ ，点 $\text{[math]}$ 在边 $\text{[math]}$ 上， $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ．
1. （1）求证：四边形 $\text{[math]}$ 是矩形；
2. （2）已知 $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 的平分线，若 $\text{[math]}$ ，求 $\text{[math]}$ 的长度．
答案解析收藏纠错 + 选题
24. (2023八下·南昌期末) 如图，在平面直角坐标系xOy中，直线y=- $\text{[math]}$ x＋8与x轴，y轴分别交于点A，点B，点D在y轴的负半轴上，若将△DAB沿直线AD折叠，点B恰好落在x轴正半轴上的点C处．
1. （1）求AB的长和点C的坐标；
2. （2）求直线CD的表达式．
答案解析收藏纠错 + 选题

25. (2021·郑州模拟) 2021年7月1日是中国共产党成立100周年纪念日．为了让全校学生牢固树立爱国爱党的崇高信念，某校开展了形式多样的党史学习教育活动．八、九年级各300名学生举行了一次党史知识竞赛后随机抽取了八、九年级各20名学生的成绩进行了整理与分析，部分信息如下：

a ．抽取九年级20名学生的成绩如下：

86	88	97	91	94	62	51	94	87	71
94	78	92	55	97	92	94	94	85	98

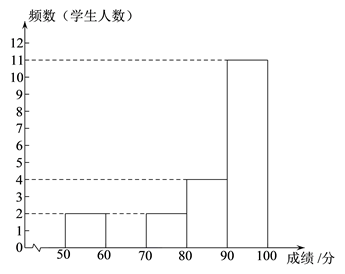
b ．抽取九年级20名学生的成绩频数分布直方图如下（数据分成5组： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）：

c ．九年级抽取的20名学生成绩的平均数、中位数、方差如下表：

年级	平均数	中位数	方差
九年级	85	m	192

请根据以上信息，回答下列问题：

（1）补全频数分布直方图，写出表中m的值；
（2）若90分及以上为优秀，估计此次知识竞赛中九年级成绩优秀的学生人数；
（3）通过分析随机抽取的八年级20名学生的成绩发现：这20名学生成绩的中位数为88，方差为80.4，且八、九两个年级随机抽取的共40名学生成绩的平均数是85.2
①求八年级这20名学生成绩的平均数；

②你认为哪个年级的成绩较好，说明理由（至少从两个不同的角度说明推断的合理性）．

答案解析收藏纠错 + 选题

26. (2021九上·北京开学考) 在平面直角坐标系 $\text{[math]}$ 中，正比例函数 $\text{[math]}$ 与反比例函数 $\text{[math]}$ 的图象相交于点 $\text{[math]}$ 与点Q．
1. （1）求点Q的坐标；
2. （2）若存在点 $\text{[math]}$ ，使得 $\text{[math]}$ ，求c的值；
3. （3）过点 $\text{[math]}$ 平行于x轴的直线，分别与第一象限内的正比例函数 $\text{[math]}$ 、反比例函数数 $\text{[math]}$ 的图象相交于点 $\text{[math]}$ 、点 $\text{[math]}$ ，当 $\text{[math]}$ 时，请直接写出a的取值范围．
答案解析收藏纠错 + 选题
27. (2021九上·北京开学考) 在正方形 $\text{[math]}$ 和正方形 $\text{[math]}$ 中， $\text{[math]}$ ，连接 $\text{[math]}$ ，H是 $\text{[math]}$ 的中点．
1. （1）如图1，若点B、D、F在同一直线上，求 $\text{[math]}$ 的长；
2. （2）在（1）条件下，连接 $\text{[math]}$ ．求线段 $\text{[math]}$ 和 $\text{[math]}$ 的数量关系和位置关系，并证明；
3. （3）如图2，正方形 $\text{[math]}$ 绕点D旋转，使得点H在线段 $\text{[math]}$ 的延长线上，连接 $\text{[math]}$ ，求 $\text{[math]}$ 的长度．
答案解析收藏纠错 + 选题
28. (2021九上·北京开学考) 定义：如果一条直线把一个平面图形的面积分成相等的两部分，我们把这条直线称为平面图形的一条面积等分线．
1. （1）如图1，已知 $\text{[math]}$ ，请用尺规作出 $\text{[math]}$ 的一条面积等分线．
2. （2）已知：如图2，在平面直角坐标系 $\text{[math]}$ 中，矩形 $\text{[math]}$ 的边 $\text{[math]}$ 在x轴的正半轴上、 $\text{[math]}$ 在y轴的正半轴上， $\text{[math]}$ ．
  ①请判断直线 $\text{[math]}$ 是否为矩形 $\text{[math]}$ 的面积等分线，并说明理由；
  
  ②若矩形 $\text{[math]}$ 的面积等分线与坐标轴所围成的三角形面积为4，请直接写出此面积等分线的函数表达式．
3. （3）如图3，在 $\text{[math]}$ 中，点A的坐标为 $\text{[math]}$ ，点B的坐标为 $\text{[math]}$ ，点C的坐标为 $\text{[math]}$ ，点D的坐标 $\text{[math]}$ ，求过点D的一条 $\text{[math]}$ 的面积等分线的解析式．
4. （4）在 $\text{[math]}$ 中点A的坐标为 $\text{[math]}$ ，点B的坐标为 $\text{[math]}$ ，点C的坐标为 $\text{[math]}$ ，直线 $\text{[math]}$ 是 $\text{[math]}$ 的一条面积等分线，请直接写出b的取值范围．
答案解析收藏纠错 + 选题