河南省郑州外国语中学2021年中考模拟四模数学试卷

更新时间：2022-04-25 浏览次数：97 类型：中考模拟

一、单选题

1. (2023·姜堰模拟) 计算 $\text{[math]}$ 的结果是（）

A . -5 B . -1 C . 1 D . 5

答案解析收藏纠错 + 选题
2. (2021·郑州模拟) 如图是由7个相同的小正方体搭成的几何体，在标号为①的小正方体上方添加一个小正方体后，所得几何体的三视图与原几何体的三视图相比没有发生变化的是（）

A . 主视图和俯视图 B . 主视图和左视图 C . 左视图和俯视图 D . 主视图和左视图

答案解析收藏纠错 + 选题
3. (2021·郑州模拟) 下列调查中，调查方式选择正确的是（）

A . 为了了解1 000个灯泡的使用寿命，选择全面调查 B . 为了了解某公园全年的游客流量，选择抽样调查 C . 为了了解生产的一批炮弹的杀伤半径，选择全面调查 D . 为了了解一批袋装食品是否含有防腐剂，选择全面调查

答案解析收藏纠错 + 选题
4. (2021·郑州模拟) 已知直线l₁∥l₂ ，一块含30°角的直角三角板如图所示放置，∠1＝35°，则∠2等于（）

A . 25° B . 35° C . 40° D . 45°

答案解析收藏纠错 + 选题
5. (2021·郑州模拟) 纳米（ $\text{[math]}$ ）是长度的单位， $\text{[math]}$ ， $\text{[math]}$ 如果将在2022年底攻克 $\text{[math]}$ 工艺芯片技术的难关，其中 $\text{[math]}$ 等于（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2021·郑州模拟) 反比例函数 $\text{[math]}$ 在第一象限的图象如图所示，则k的值可能是（）

A . 3 B . 5 C . 6 D . 8

答案解析收藏纠错 + 选题
7. (2022·南宁模拟) 把 $\text{[math]}$ 这 $\text{[math]}$ 个数填入 $\text{[math]}$ 方格中，使其任意一行，任意一列及两条对角线上的数之和都相等，这样便构成了一个“九宫格”.它源于我国古代的“洛書”（图 $\text{[math]}$ ），是世界上最早的“幻方”.图 $\text{[math]}$ 是仅可以看到部分数值的“九宫格”，则其中 $\text{[math]}$ 的值为（）

A . 1 B . 3 C . 4 D . 6

答案解析收藏纠错 + 选题
8. (2022九上·深圳月考) 关于x的一元二次方程x²﹣4x+2n＝0无实数根，则一次函数y＝（2﹣n）x+n的图象不经过（　　）

A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限

答案解析收藏纠错 + 选题
9. (2021八下·沧县期中) 如图，在四边形ABCD中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .分别以点A，C为圆心，大于 $\text{[math]}$ 长为半径作弧，两弧交于点E，作射线BE交AD于点F，交AC于点O.若点O是AC的中点，则CD的长为（）

A . $\text{[math]}$ B . 4 C . 3 D . $\text{[math]}$

答案解析收藏纠错 + 选题
10. (2021·郑州模拟) 如图，正方形ABCD的四个顶点均在坐标轴上.已知点A(﹣2，0)、E(﹣3，0)，点P是正方形ABCD边上的一个动点，在正方形ABCD外作等腰直角 $\text{[math]}$ PEF，若点P从点A出发，以每秒 $\text{[math]}$ 个单位长度沿A→D→C→B→A方向运动，则第2020秒时，点F的坐标为（）

A . (﹣4，4) B . (5，﹣3) C . (﹣3，5) D . (﹣4，2)

答案解析收藏纠错 + 选题

二、填空题

11. (2023八下·铜梁期末) 计算： $\text{[math]}$ .

答案解析收藏纠错 + 选题
12. (2023八下·凤翔期末) 不等式组 $\text{[math]}$ 的所有整数解的积是．

答案解析收藏纠错 + 选题
13. (2023·光明模拟) 在一个不透明的口袋中装有4个只有颜色不同的球，其中红球1个，白球2个，黄球1个，搅匀后随机摸出两个球，恰好都是白球的概率是

答案解析收藏纠错 + 选题
14. (2021·郑州模拟) 如图，AC是半圆O的一条弦，将弧AC以弦AC为折线折叠后过圆心O，图中阴影部分的面积为 $\text{[math]}$ ，则⊙O的半径为 .

答案解析收藏纠错 + 选题
15. (2023九上·永嘉期末) 如图，已知A、B两点的坐标分别为(-8，0)、(0，8)，点C、F分别是直线x=5和x轴上的动点，CF=10，点D是线段CF的中点，连接AD交y轴于点E，当 $\text{[math]}$ ABE的面积取得最小值时，tan∠BAD=.

答案解析收藏纠错 + 选题

三、解答题

16. (2021·郑州模拟) 下面是小斌同学进行分式化简的过程，请认真阅读并解答问题.
$\text{[math]}$ $\text{[math]}$

= $\text{[math]}$      第一步

= $\text{[math]}$                  第二步

= $\text{[math]}$              第三步

= $\text{[math]}$                   第四步

= $\text{[math]}$                          第五步

= $\text{[math]}$                          第六步
1. （1）填空：
  a.以上化简步骤中，第步是进行分式的通分，通分的依据是
  
  b.第步开始出现错误，这一步错误的原因是① ， ②.
2. （2）请直接写出该分式化简后的正确结果.
3. （3）除纠正上述错误外，请你根据平时的学习经验，就分式化简时还需要注意的事项给其他同学提一条建议.
答案解析收藏纠错 + 选题

17. (2021·郑州模拟) 2021年7月1日是中国共产党成立100周年纪念日．为了让全校学生牢固树立爱国爱党的崇高信念，某校开展了形式多样的党史学习教育活动．八、九年级各300名学生举行了一次党史知识竞赛后随机抽取了八、九年级各20名学生的成绩进行了整理与分析，部分信息如下：

a ．抽取九年级20名学生的成绩如下：

86	88	97	91	94	62	51	94	87	71
94	78	92	55	97	92	94	94	85	98

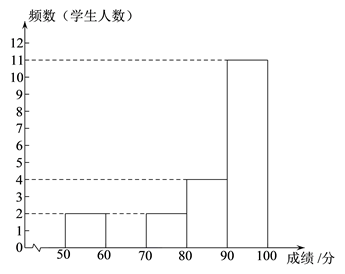
b ．抽取九年级20名学生的成绩频数分布直方图如下（数据分成5组： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）：

c ．九年级抽取的20名学生成绩的平均数、中位数、方差如下表：

年级	平均数	中位数	方差
九年级	85	m	192

请根据以上信息，回答下列问题：

（1）补全频数分布直方图，写出表中m的值；
（2）若90分及以上为优秀，估计此次知识竞赛中九年级成绩优秀的学生人数；
（3）通过分析随机抽取的八年级20名学生的成绩发现：这20名学生成绩的中位数为88，方差为80.4，且八、九两个年级随机抽取的共40名学生成绩的平均数是85.2
①求八年级这20名学生成绩的平均数；

②你认为哪个年级的成绩较好，说明理由（至少从两个不同的角度说明推断的合理性）．

答案解析收藏纠错 + 选题

18. (2021·郑州模拟) 停车难已成为合肥城市病之一，主要表现在居住停车位不足，停车资源结构性失衡，中心城区供需差距大等等.如图是张老师的车与墙平行停放的平面示意图，汽车靠墙一侧OB与墙MN平行且距离为0.8米，已知小汽车车门宽AO为 1.2 米，当车门打开角度∠AOB为40°时，车门是否会碰到墙？请说明理由.（参考数据：sin 40°≈0.64，cos 40°≈0.77，tan 40°≈0.84）

答案解析收藏纠错 + 选题
19. (2021·郑州模拟) 如图①，一个正方体铁块放置在圆柱形水槽内，现以一定的速度往水槽中注水，28s时注满水槽．水槽内水面的高度y（cm）与注水时间x（s）之间的函数图象如图②所示．
1. （1）正方体的棱长为cm；
2. （2）求线段AB对应的函数解析式，并写出自变量x的取值范围；
3. （3）如果将正方体铁块取出，又经过t（s）恰好将此水槽注满，直接写出t的值．
答案解析收藏纠错 + 选题

20. (2021·郑州模拟) 阅读下列材料，完成相应的任务

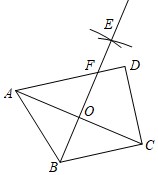
婆罗摩笈多（Brahmagupta）是古印度著名数学家、天文学家，他在三角形、四边形、零和负数的算术运算规则、二次方程等方面均有建树，特别是在研究一阶和二阶不定方程方面作出了巨大贡献.他曾经提出了“婆罗摩笈多定理”，该定理也称为“古拉美古塔定理”.该定理的内容及部分证明过程如下：

古拉美古塔定理：已知：如图，四边形ABCD内接于⊙O，对角线AC⊥BD，垂足为M，直线ME⊥BC，垂足为E，并且交直线AD于点F，则AF＝FD.

证明：∵AC⊥BD，ME⊥BC

∴∠CME+∠C＝90°，∠CBD+∠C＝90°

∴∠CBD＝∠CME

∴________ ， ∠CME＝∠AMF

∴∠CAD＝∠AMF

∴AF＝MF

…

任务：

（1）材料中划横线部分短缺的条件为：；
（2）请用符号语言将下面“布拉美古塔定理”的逆命题补充完整，并证明该逆命题的正确性：
已知：如图，四边形ABCD内接于⊙O，对角线AC⊥BD，垂足为M，F为AD上一点，直线FM交BC于点E，

①▲ .

求证：②▲ .

证明：

答案解析收藏纠错 + 选题

21. (2021·郑州模拟) 在平面直角坐标系 $\text{[math]}$ 中，抛物线 $\text{[math]}$ 经过点 $\text{[math]}$ .
1. （1）用含b的代数式表示抛物线顶点的坐标；
2. （2）若抛物线经过点 $\text{[math]}$ ，且满足 $\text{[math]}$ ，求n的取值范围；
3. （3）若 $\text{[math]}$ 时， $\text{[math]}$ ，结合函数图象，直接写出b的取值范围.
答案解析收藏纠错 + 选题
22. (2021·郑州模拟) 如图1，小明用一张边长为 $\text{[math]}$ 的正三角形硬纸板设计一个无盖的正三棱柱糖果盒，从三个角处分别剪去一个形状大小相同的四边形，其一边长记为 $\text{[math]}$ ，再折成如图2所示的无盖糖果盒，它的容积记为 $\text{[math]}$ .
1. （1） $\text{[math]}$ 关于 $\text{[math]}$ 的函数关系式是，自变量 $\text{[math]}$ 的取值范围是.
2. （2）为探究 $\text{[math]}$ 随 $\text{[math]}$ 的变化规律，小明类比二次函数进行了如下探究：
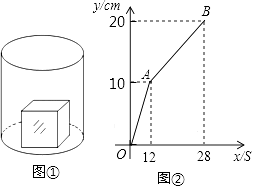
  ①列表：请你补充表格中的数据：
  
  $\text{[math]}$
  
  0
  
  0.5
  
  1
  
  1.5
  
  2
  
  2.5
  
  3
  
  $\text{[math]}$
  
  0
  
  3.125
  
  3.375
  
  0.625
  
  0
  
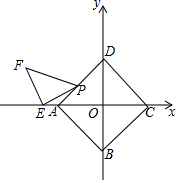
  ②描点：请你把上表中各组对应值作为点的坐标，在平面直角坐标系中描出相应的点；
  
  ③连线：请你用光滑的曲线顺次连接各点.
3. （3）利用函数图象解决：
  ①该糖果盒的最大容积是 ▲ ；
  
  ②若该糖果盒的容积超过 $\text{[math]}$ ，请估计糖果盒的底边长 $\text{[math]}$ 的取值范围.（保留一位小数）
答案解析收藏纠错 + 选题
23. 阅读材料：平面几何中的费马问题是十七世纪法国数学家、被誉为业余数学家之王的皮埃尔·德·费马提出的一个著名的几何问题.1643年，在一封写给意大利数学家和物理学家托里拆利的私人信件中，费马提出了下面这个极富挑战性和趣味性的几何难题，请求托里拆利帮忙解答：给定不在一条直线上的三个点A，B，C，求平面上到这三个点的距离之和最短的点P的位置.托里拆利成功地解决了费马的问题.后来人们就把平面上到一个三角形的三个顶点A，B，C距离之和最小的点称为 $\text{[math]}$ ABC的费马-托里拆利点，也简称为费马点或托里拆利点.问题解决：
1. （1）费马问题有多种不同的解法，最简单快捷的还是几何解法.如图1，我们可以将 $\text{[math]}$ BPC绕点B顺时针旋转60°得到 $\text{[math]}$ BDE，连接PD，可得 $\text{[math]}$ BPD为等边三角形，故PD=PB，由旋转可得DE=PC，因PA+PB+PC=PA+PD+DE，由可知，PA+PB+PC的最小值与线段的长度相等；
2. （2）如图2，在直角三角形ABC内部有一动点P，∠BAC=90°，∠ACB=30°，连接PA，PB，PC，若AB=2，求PA+PB+PC的最小值；
3. （3）如图3，菱形ABCD的边长为4，∠ABC=60°，平面内有一动点E，在点E运动过程中，始终有∠BEC=90°，连接AE、DE，在 $\text{[math]}$ ADE内部是否存在一点P，使得PA+PD+PE最小，若存在，请直接写出PA+PD+PE的最小值；若不存在，请说明理由.
答案解析收藏纠错 + 选题