2021年秋季浙教版数学八年级上学期期中测试模拟卷（适合宁波...

更新时间：2021-10-25 浏览次数：163 类型：期中考试

一、单选题

1. (2021·桂林) 下列图形中，是轴对称图形的是（）

A . B . C . D .

答案解析收藏纠错 + 选题
2. (2021·宜宾) 若长度分别是a、3、5的三条线段能组成一个三角形，则a的值可以是（）

A . 1 B . 2 C . 4 D . 8

答案解析收藏纠错 + 选题
3. (2020八下·南昌月考) 如图所示，点 $\text{[math]}$ 的表示的数为 $\text{[math]}$ ， $\text{[math]}$ ，以 $\text{[math]}$ 为圆心， $\text{[math]}$ 为半径画弧，交数轴于点 $\text{[math]}$ ，则点 $\text{[math]}$ 表示的数是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
4. (2016八上·海盐期中) 对假命题“任何一个角的补角都不小于这个角”举反例，正确的反例是（　　)

A . ∠α=60°，∠α的补角∠β=120°，∠β＞∠α B . ∠α=90°，∠α的补角∠β=90°，∠β=∠α C . ∠α=100°，∠α的补角∠β=80°，∠β＜∠α D . 两个角互为邻补角

答案解析收藏纠错 + 选题
5. (2021七下·涵江期末) 若 $\text{[math]}$ ，则下列不等式一定成立的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
6. (2021八下·广水期末) 已知△ABC中，a、b、c分别是∠A、∠B、∠C的对边，下列条件中不能判断△ABC是直角三角形的是（）

A . ∠A：∠B：∠C＝3：4：5 B . ∠C＝∠A﹣∠B C . a²+b²＝c² D . a：b：c＝6：8：10

答案解析收藏纠错 + 选题
7. (2021八上·兴宁月考) 如图，BC∥EF ， BC＝EF ，要使得△ABC≌△DEF ，需要补充的条件不能是（）

A . ∠B＝∠E B . AB＝DE C . AD＝CF D . AB∥DE

答案解析收藏纠错 + 选题
8. (2021九上·娄底月考) 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 边上的高， $\text{[math]}$ ，则下列结论中正确的是（）

A . $\text{[math]}$ B . $\text{[math]}$ C . $\text{[math]}$ D . $\text{[math]}$

答案解析收藏纠错 + 选题
9. (2018八上·柯桥期中) 如图，由4个相同的直角三角形与中间的小正方形拼成一个大正方形，若大正方形面积是9，小正方形面积是1，直角三角形较长直角边为a，较短直角边为b，则ab的值是（）

A . 4 B . 6 C . 8 D . 10

答案解析收藏纠错 + 选题
10. (2020八上·镇海期中) 如图：在△ABC中，∠B=45°，D是AB边上一点，连接CD，过A作AF⊥CD交CD于G，交BC于点F.已知AC=CD，CG=3，DG=1，则下列结论正确的是（）

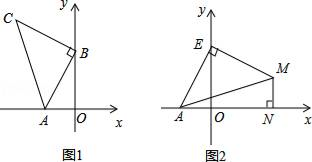
①∠ACD=2∠FAB ② $\text{[math]}$ ③ $\text{[math]}$ ④ AC=AF

A . ①②③ B . ①②③④ C . ②③④ D . ①③④

答案解析收藏纠错 + 选题

二、填空题

11. (2021七下·德阳期末) 不等式2x﹣1≤3x+2的负整数解的和是 .

答案解析收藏纠错 + 选题
12. (2021八下·江北期末) 在 $\text{[math]}$ 中，两直角边的长分别为7和24，则其斜边上的中线长为.

答案解析收藏纠错 + 选题
13. (2021·襄阳) 不等式组 $\text{[math]}$ 的解集是.

答案解析收藏纠错 + 选题
14. (2021七下·于洪期末) 如图，点P是∠AOB内任意一点，OP＝9，M、N分别是射线OA和OB上的动点，若△PMN周长的最小值为9，则∠AOB＝°．

答案解析收藏纠错 + 选题
15. (2021七上·文登期末) $\text{[math]}$ 为等边三角形，点D为 $\text{[math]}$ 边上一点，以 $\text{[math]}$ 为边做等边三角形 $\text{[math]}$ ，使点E，A在直线 $\text{[math]}$ 的同侧，连接 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为．

答案解析收藏纠错 + 选题
16. (2021八上·诸暨月考) 如图所示，∠E＝∠F＝90°，∠B＝∠C ， AE＝AF ．给出下列结论：①∠1＝∠2；②BE＝CF；③△ACN≌△ABM；④CD＝DN ．其中正确的结论是．（将你认为正确的结论的序号都填上）

答案解析收藏纠错 + 选题

三、解答题

17. (2021七下·潼南期末) 解不等式（组）：
1. （1）解不等式 $\text{[math]}$
2. （2）解不等式组： $\text{[math]}$
答案解析收藏纠错 + 选题
18. (2020八上·义乌期末) （阅读）例题：在等腰三角形 $\text{[math]}$ 中，若 $\text{[math]}$ ，求 $\text{[math]}$ 的度数.
点点同学在思考时是这样分析的： $\text{[math]}$ ， $\text{[math]}$ 都可能是顶角或底角，因此需要进行分类.他认为画“树状图”可以帮我们不重复，不遗漏地分类（如图），据此可求出 $\text{[math]}$ 的度数.
1. （1）（解答）
  由以上思路，可得 $\text{[math]}$ 的度数为；
2. （2）（应用）
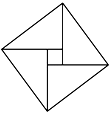
  将一个边长为5，12，13的直角三角形拼上一个三角形后可以拼成一个等腰三角形，图2就是其中的一种拼法.请你利用备用图画出三种可能的情形，使得拼成的等腰三角形腰长为13.
  
  （注意：请对所拼成图形中的线段长度标注数据）
答案解析收藏纠错 + 选题
19. (2021八上·微山月考) 如图，在△ABC中，AB=AC ， ∠BAC=90°，分别过点B ， C向过点A的直线作垂线，垂足分别为点E ， F ．

求证：
1. （1） △ABE≌△CAF；
2. （2） EF=BE+CF ．
答案解析收藏纠错 + 选题
20. (2019八上·海安月考) 如图1，A（﹣2，0），B（0，4），以B点为直角顶点在第二象限作等腰直角△ABC.
1. （1）求C点的坐标；
2. （2）在坐标平面内是否存在一点P，使△PAB与△ABC全等？若存在，求出P点坐标，若不存在，请说明理由；
3. （3）如图2，点E为y轴正半轴上一动点，以E为直角顶点作等腰直角△AEM，过M作MN⊥x轴于N，求OE﹣MN的值.
答案解析收藏纠错 + 选题
21. (2021八上·长沙开学考) 现计划把甲种货物306吨和乙种货物230吨运往某地.已知有A、B两种不同规格的货车共50辆，如果每辆A型货车最多可装甲种货物7吨和乙种货物3吨，每辆B型货车最多可装甲种货物5吨和乙种货物7吨.
1. （1）装货时按此要求安排A、B两种货车的辆数，共有几种方案？
2. （2）使用A型车每辆费用为600元，使用B型车每辆费用800元.在上述方案中，哪个方案运费最省？最省的运费是多少元？
3. （3）在（2）的方案下，现决定对货车司机发共2100元的安全奖，已知每辆A型车奖金为m元.每辆B型车奖金为n元，38＜m＜n.且m、n均为整数，求此次奖金发放的具体方案.
答案解析收藏纠错 + 选题
22. (2021八上·盐都期末) 在四边形 $\text{[math]}$ 中，已知 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ .
1. （1）连接 $\text{[math]}$ ，试判断 $\text{[math]}$ 的形状，并说明理由；
2. （2）求 $\text{[math]}$ 的度数
答案解析收藏纠错 + 选题
23. 图①是美丽的弦图，包含四个全等的直角三角形．
1. （1）弦图中包含了一大一小两个正方形，已知每个直角三角形较长的直角边长为a，较短的直角边长为b，斜边长为c，结合图①，试验证勾股定理；
2. （2）如图②，将这四个直角三角形紧密拼接，形成飞镖状，已知外围轮廓(实线)的周长为24，OC=3，求该飞镖状图案的面积；
3. （3）如图③，将八个全等的直角三角形紧密拼接，记正方形ABCD，正方形EFGH，正方形MNKT的面积分别为S₁ ， S₂ ， S₃ ，若S₁+S2+S₃=16，则S₂=．
答案解析收藏纠错 + 选题
24. (2021八上·武汉期末) 已知 $\text{[math]}$ 是等边三角形，点D是AC的中点，点E在射线BC上，点F在射线BA上， $\text{[math]}$ ．
1. （1）如图1，若点F与B点重合，求证： $\text{[math]}$ ；
2. （2）如图2，若点E在线段BC上，点F在线段BA上，求 $\text{[math]}$ 的值；
3. （3）如图3，若 $\text{[math]}$ ，直接写出 $\text{[math]}$ 的度数为．
答案解析收藏纠错 + 选题