 B .
B .  C .
C .  D .
D . 
⑴以点C为圆心,作能与直线 相交于D、E点的圆弧.
⑵分别以点D和点E为圆心, 长为半径作圆弧,两弧交于点F,连结
、
.
⑶作直线 交
于点G.
根据以上作图过程及所作图形,有如下结论:① ;②
;③
;④
.其中正确的结论是( )


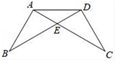
(1)AB=DC,(2)BE=CE , (3)∠B=∠C , (4)∠BAE=∠CDE
要求同学从这四个等式中选出两个作为条件,推出△AED是等腰三角形,请你试着完成王老师提出的要求,并说明理由.已知:
求证:△AED是等腰三角形.

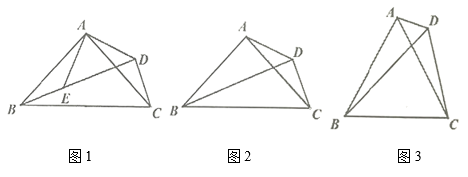
① 的度数为;
② ,
,
之间的关系是.