
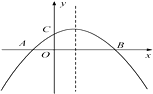



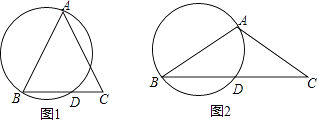

①求证: ;
②若 ,求线段
的长.


小明通过观察、分析、思考,形成了如下思路:
思路一:将△BPC绕点B逆时针旋转90°,得到△BP′A,连接PP′,求出∠APB的度数;
思路二:将△APB绕点B顺时针旋转90°,得到△CP'B,连接PP′,求出∠APB的度数.
请参考小明的思路,任选一种写出完整的解答过程.


如下图,抛物线F2都是抛物线F1的过顶抛物线,设F1的顶点为A,F2的对称轴分别交F1、F2于点D、B,点C是点A关于直线BD的对称点.
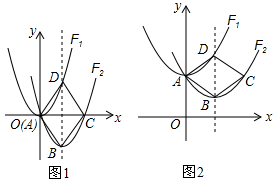
①a=,b=.
②如果顺次连接A、B、C、D四点,那么四边形ABCD为( )
A.平行四边形 B.矩形 C.菱形 D.正方形