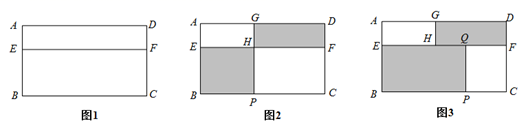
⑴利用图①、图②中图形的面积关系分别写出能解释的乘法公式；
⑵图③是用四个长和宽分别为a、b的全等的长方形拼成的一个正方形(所拼图形无重叠无缝隙)，直接写出式子(a+b)2、(a-b)2、ab之间的等量关系；
①当a+b= 5，ab=-1时，求a-b的值；
②设A= ，B=a-3，化简：(A+B)2-(A-B)2
计算：
甲：我的卡片上写着整式 ，加上整式C后得到最简整式D；
乙：我用最简整式B加上整式C得到整式 ．
根据以上信息，解答下列问题：
x+2）（x2﹣x）．她发现第一个因式的一次项系数被墨水遮挡住了．
第一步
第二步
第三步
任务1：填空：
①以上化简步骤中，第一步的依据是．
②以上化简步骤中，第步开始出现下午，这一步错误的原因是．
已知 ，
，
，求
的值．
先观察下面给出的等式，探究其隐含的规律，然后回答问题： ；
；
；
根据上面探索的规律，解决下面的问题：
解关于 的分式方程：
．
如图2，上面窗户的遮阳帘水平方向向左拉伸2a至GH ． 当下面窗户的遮阳帘水平方向向右拉伸2b时，恰好与GH在同一直线上（即点G、H、P在同一直线上）．
（问题探究）为了解决上面的数学问题，我们采取一般问题特殊化的策略，先从最简单情形入手，再逐次递进，最后猜想得出结论．
探究一：如图1，一个圆能把平面分成2个区域．
探究二：用2个圆最多能把平面分成几个区域？
如图2，在探究一的基础上，为了使分成的区域最多，应使新增加的圆与前1个圆有2个交点，将新增加的圆分成2部分，从而增加2个区域，所以，用2个圆最多能把平面分成4个区域．
探究三：用3个圆最多能把平面分成几个区域？
如图3，在探究二的基础上，为了使分成的区域最多，应使新增加的圆与前2个圆分别有2个交点，将新增加的圆分成 部分，从而增加4个区域，所以，用3个圆最多能把平面分成8个区域．
仿照前面的探究方法，写出解答过程，不需画图．
为了使分成的区域最多，应使新增加的圆与前 个圆分别有2个交点，将新增加的圆分成部分，从而增加个区域，所以，用n个圆最多能把平面分成个区域．（将结果进行化简）
①用10个圆最多能把平面分成个区域；
②用个圆最多能把平面分成422个区域．
